Le relazioni che intercorrono tra il tipo di variabile, il processo mediante il quale viene ottenuto il dato, la modalità di espressione del dato e il tipo di scala nella quale il dato viene espresso forniscono la definizione operativa delle scale di misura.
Questa definizione deriva dalla loro definizione metrologica prevista nel Sistema internazionale di unità (SI), che l'Italia nel 1982 ha adottato per legge, aggiornandolo successivamente con le modifiche via via apportate [1].
Le generalità del SI sono riportate nella brochure pubblicata dal Bureau international des poids et mesures (BIPM) [2] mentre il glossario del processo di misura è riportato nel VIM, il Vocabolario Internazionale di Metrologia [3], nel quale le scale di misura sono così definite:
→ scala di riferimento convenzionale – scala di valori definita mediante un accordo ufficiale [VIM 1.29]
→ scala ordinale – scala di valori per una grandezza ordinale [VIM 1.28]
→ scala di valori o scala di misura – insieme ordinato dei valori di grandezze di una data natura, utilizzato per classificare le grandezze di quella natura in ordine crescente o decrescente in base alle loro espressioni quantitative [VIM 1.27]
Quindi la definizione operativa delle scale di misura, a parte semplificare, ma senza cambiarne il senso, la definizione della "scala di riferimento convenzionale" riportandola da un "accordo ufficiale" al caso delle meno burocratiche, universalmente impiegate e più immediatamente intuitive scale nominali, riprende tal quale la definizione delle scale ordinali e semplicemente suddivide le scale numeriche, lasciandone immodificata la definizione metrologica riportata dal VIM, in discrete e in continue in base al processo mediante il quale è ottenuto il dato: conteggio o misura [4]. Questa suddivisione trova ulteriore supporto nel fatto che il processo di conteggio fornisce risultati espressi sotto forma di numeri interi e di una sola unità di misura (“uno”) basata sulla grandezza “numero di entità” che non ha dimensioni [VIM 1.4 e 1.8], mentre il processo di misura fornisce risultati espressi sotto forma di numeri razionali e di differenti unità di misura (metro, secondo, kilogrammo, eccetera) basate su grandezze (lunghezza, tempo, massa e quant’altro) che hanno una dimensione fisica [VIM 1.7].
Ma a questo punto la domanda è inevitabile: se esistono definizioni ufficiali, ampiamente condivise e addirittura normate, dalle quali è possibile trarre una definizione operativa piuttosto chiara che le collega ai processi di misura impiegati nella pratica, perché si trova riportato quasi dappertutto che le scale di misura sono classificate in: scale nominali, scale ordinali, scale a intervalli, scale a rapporti ?
La risposta è: per qualche ragione imperscrutabile, probabilmente potenziata dalla disponibilità del copia-e-incolla, un meme è riuscito a moltiplicarsi in modo virale fino ad occupare quasi completamente l'infosfera concernente questo argomento. E senza ragione, senza un razionale.
La proposta di suddivisione in scale nominali, scale ordinali, scale a intervalli, scale a rapporti è riportata in un lavoro del 1946 di S. S. Stevens [5], che proprio all'inizio del lavoro scrive: "PER SETTE ANNI UN COMITATO dell'Associazione britannica per l'avanzamento della scienza ha dibattuto il problema della misurazione. Nominato nel 1932 a rappresentare la Sezione A (Matematica e scienze fisiche) e Sezione J (Psicologia), il comitato è stato incaricato di considerare e riferire sulla possibilità di "stime quantitative di eventi sensoriali", che significano semplicemente: è possibile misurare le sensazioni umane? La riflessione ha portato solo al disaccordo, soprattutto su cosa si intende con il termine misurazione" [6].
La domanda che Stevens si pone "è possibile misurare le sensazioni umane?" sarà pure lecita, ma non si possono avere dubbi "su cosa si intende con il termine misurazione".
Una misurazione o procedimento di misura consiste nell'esprimere una grandezza in modo quantitativo, mediante un "valore numerico" che è un numero puro uguale al rapporto tra il "(valore della) grandezza (in esame)" e il valore di una grandezza di riferimento ad essa omogenea definita come "unità di misura", ed è quindi
(valore della) grandezza (in esame) / unità di misura = valore numerico
Corollario: il risultato di una misura ovvero il "(valore della) grandezza (in esame)" è dato dal prodotto di un "valore numerico" per la "unità di misura"
(valore della) grandezza (in esame) = valore numerico · unità di misura
Per indicare il prodotto, rendendo "valore numerico" e "unità di misura" un tutt'uno inscindibile, il simbolo del prodotto [ · ] per convenzione viene sostituito con lo spazio unificatore [7], come avviene ad esempio in 2.5 m, 12 s, 75 kg (unica eccezione sono le unità angolari, per le quali lo spazio tra il valore numerico e il simbolo dell'unità non è previsto, pertanto un angolo verrà riportato, ad esempio, come 41°54'39).
Il lavoro di Stevens è viziato da un errore concettuale di fondo: nel tentativo di "misurare le sensazioni umane" e dare dignità di "misura" ai risultati dei metodi di ricerca in psicologia, ha cercato di adattare alla psicologia "... il termine misurazione..." – che ha e deve avere una definizione univoca – pensando di risolvere il problema con nuove definizioni delle scale di misura, mentre avrebbe dovuto ricercare la "... possibilità di "stime quantitative di eventi sensoriali"..." in una qualche grandezza [VIM 1.1] e nella sua unità di misura [VIM 1.9], perché senza il fondamento di grandezze [misurabili] e delle loro unità di misura, le scale di misura [VIM 1.27] sono una espressione vuota.
Quindi mentre per misura [VIM 2.1] e per tutti gli altri termini che devono essere impiegati per esprimersi correttamente in campo scientifico (ma anche nella vita di tutti i giorni) rimando al SI e alle definizioni del VIM, qui mi limito a rilevare che la forzatura impiegata da Stevens per accreditare le misure in campo psicologico ha determinato solamente confusione terminologica, anticamera della confusione concettuale [8].
Se proprio si vuole ricollegare la definizione di Stevens delle scale di misura – inutile dire che è fortemente sconsigliata anche in campo psicologico, al quale nulla aggiunge rispetto alle scale ufficiali qui trattate: in ogni caso il VIM semplicemente la ignora – alla definizione operativa delle scale di misura in campo scientifico, e con questa alla loro definizione metrologica, basta notare che:
- se i dati sono espressi in una scala numerica discreta possiamo avere:
[A] quella che Stevens denomina scala a intervalli quando, come accade ad esempio per le date, non sono possibili rapporti (non posso dividere il 28 febbraio per il 2 febbraio) ma posso solamente calcolare l'intervallo che le separa (nel caso specifico 26 giorni);
[B] quella che Stevens denomina scala a rapporti quando, come accade ad esempio per il numero di auto ferme al semaforo, se prima ne ho contate 5 e dopo ne ho contate 4, oltre a calcolare la differenza posso calcolare anche il rapporto prima-dopo che è 1.25;
- se i dati sono espressi in una scala numerica continua possiamo avere:
[A] quella che Stevens denomina scala a intervalli quando, come accade ad esempio per la temperatura in gradi Celsius (°C), posso dire che tra la temperatura di +20 °C e la temperatura di -10 °C c'è un intervallo di 30 °C, ma non posso dividere la prima per la seconda;
[B] quella che Stevens denomina scala a rapporti quando, come accade ad esempio per la concentrazione del colesterolo nel siero, posso calcolare non solo l'intervallo tra due valori (la mia concentrazione di colesterolo è 220 mg/dL, la tua 110 mg dL, la differenza è di 110 mg/dL) ma anche il rapporto (la mia concentrazione del colesterolo è 2.0 volte la tua).
Questo significa che (tolte le scale nominali e le scale ordinali sulle quali tutti concordano) quelle di Stevens non sono scale di misura ma, nella migliore e proprio nella migliore delle ipotesi, potrebbero (e uso il condizionale) essere considerate un attributo aggiuntivo (ma privo di interesse metrologico) delle scale numeriche. Riprendiamo quindi la nostra definizione operativa delle scale di misura, che trova un fondamento nel SI e nel VIM e che fornisce il razionale su cui si fondano le modalità di rappresentazione grafica e di analisi statistica dei dati.
Il tipo più semplice di scala è rappresentato dalla scala nominale. Corrisponde ai dati della natura più elementare, quella di dati qualitativi per i quali è disponibile solamente una descrizione verbale. Ne sono un esempio la classificazione maschio / femmina, la classificazione dei gruppi sanguigni ABO (O, A, B, AB), dei motori (endotermici, esotermici, elettrici, eccetera), delle specie animali (ad esempio: cane domestico, sciacallo, coyote, lupo, dingo) e così via. La misura più intuitiva e più utilizzata, nel caso della scala nominale, è costituita dalla percentuale (o dalla proporzione o frazione). In questo caso le rappresentazioni che si possono impiegare sono il grafico a torta (pie-chart) e, quando le grandezze da rappresentare sono indipendenti e non costituiscono la parte di un tutto, il grafico a barre (barplot) con le barre staccate e disposte orizzontalmente.
Nel caso di dati qualitativi per i quali è disponibile una descrizione sotto forma di attributo ordinabile si ha a che fare con una scala ordinale. Questo avviene per esempio per la classificazione in neonati, bambini e adulti, nella quale è appropriato applicare un ordinamento crescente per classi di età (neonato < bambino < adulto), per il livello di scolarità (scuola elementare < scuola media < diploma < laurea), eccetera. Un altro esempio è la classificazione per ranghi, nella quale il valore osservato viene trasformato nel corrispondente rango, cioè nel numero della posizione che il dato occupa nella lista ordinata dei dati. Così la classificazione inadeguato / parzialmente adeguato / adeguato / più che adeguato / eccellente può essere trasformata nella classificazione 1 / 2 / 3 / 4 / 5. Per le scale ordinali è possibile utilizzare un grafico a torta (pie-chart) oppure, per valorizzare la possibilità di ordinamento delle classi, un grafico a barre (barplot) con le barre staccate per indicare la discontinuità.
Una scala numerica discreta è tipicamente quella relativa a dati numerici ottenuti mediante operazioni di conteggio e riportati sotto forma di interi o numeri naturali (1, 2, 3, ….). Si prenda ad esempio il conteggio degli eritrociti (globuli rossi) nel sangue. La differenza minima tra due conteggi teoricamente misurabile è rappresentata da un globulo rosso: i dati sono numerici, ma tra l'uno l'altro non esistono valori intermedi. Altri esempi di scala numerica discreta sono il numero di controlli medici effettuati da una donna durante la gravidanza, il numero di insegnanti di ruolo nel liceo vicino a casa, il numero di auto ferme al semaforo e così via. Per le scale numeriche discrete si possono utilizzare un grafico a barre (barplot) con le barre staccate per indicare la discontinuità ma non l'istogramma che è basato sull'ipotesi di continuità dei dati, o anche, nel caso in cui si debbano rappresentare contemporaneamente due variabili, un grafico di dispersione (grafico xy o grafico cartesiano o scatterplot) precisando che i valori compresi tra due interi non hanno un corrispettivo reale.
La scala numerica continua è tipicamente quella impiegata per rappresentare dati numerici ottenuti mediante procedimenti di misura come quelli chimici e quelli fisici e i cui dati sono riportati sotto forma di numeri razionali (1.435, 123.9, 84.327, ...). Esempi ne sono la misura della concentrazione del colesterolo nel sangue, la misura della distanza tra due luoghi, la misura della velocità di un'auto, la misura del peso di una persona e quant'altro. L'intervallo tra due valori può essere suddiviso a piacere, anche se non oltre i limiti del potere di risoluzione degli strumenti di misura, che impongono nella pratica un numero molto limitato di cifre significative. Per le scale numeriche continue è possibile impiegare di volta in volta il classico istogramma, un grafico a linee spezzate come un poligono di frequenza, o ancora un grafico di dispersione (grafico xy o grafico cartesiano o scatterplot) nel caso in cui si debbano rappresentare contemporaneamente due variabili.
Dal punto di vista della statistica, ai dati espressi in forma di scale nominali sono applicabili i test basati sulla enumerazione dei casi (come test chi-quadrato, test di Fisher, test di McNemar), ai dati espressi in forma di scale ordinali sono applicabili in aggiunta i test basati sui ranghi, mentre ai dati espressi in forma di scale numeriche sono applicabili, con la necessaria appropriatezza e le dovute attenzioni, i test basati sulle ipotesi di continuità e gaussianità delle distribuzioni (test parametrici), i test non parametrici e i test basati su modelli bayesiani.
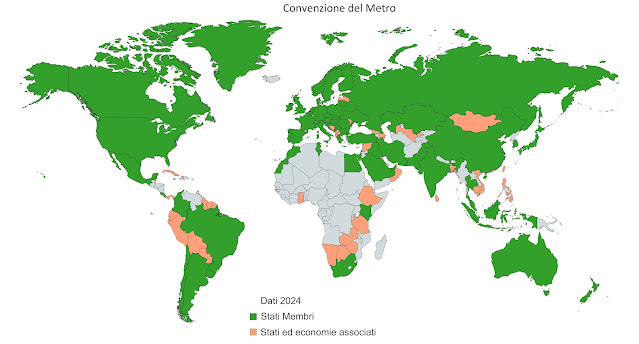
La conclusione? Molto semplice. Siglata per la prima volta a Parigi il 20 maggio 1875 da 17 Stati [9] la Convenzione del metro, che originariamente prevedeva l'impiego del Sistema metrico decimale che si è poi evoluto nel Sistema internazionale di unità, secondo i dati ufficiali forniti dal BIPM all'inizio del 2024 contava 64 Stati Membri [10] e 36 Stati ed economie associati [11].
Considerato che tutte le nazioni più popolose, incluse Cina e India, vi aderiscono, il SI con le sue grandezze e unità di misura è diventato un comune denominatore e un riferimento per miliardi di persone, nella scienza ma anche nella vita quotidiana [12].
Tra i documenti che il SI mette a disposizione perché ci si possa avvicinare in modo adeguato al mondo delle misure, il Vocabolario Internazionale di Metrologia riveste un ruolo cruciale: e questo post vuole essere un invito a consultarlo per formare, per informare, per adeguare i nostri modi di riportare i dati ed esprimerci con la necessaria appropriatezza quando parliamo di misure.
Nota bene: in R il separatore delle cifre decimali è il punto (.) e come già riportato altrove questa convenzione per ragioni di omogeneità viene adottata negli script, nei file di dati e nel testo dei post.
----------
[1] Il Sistema Internazionale di unità (SI) diviene legale in Italia nel 1982, le successive modifiche sono recepite nel 2001, nel 2009 e nel 2020, questa è la normativa aggiornata a inizio 2024, che include la correzione riportata a livello comunitario nel 1984:
- DECRETO DEL PRESIDENTE DELLA REPUBBLICA 12 agosto 1982, n. 802. Attuazione della direttiva (CEE) n. 80/181 relativa alle unita' di misura. GU Serie Generale n.302 del 03-11-1982 - Suppl. Ordinario.
https://www.gazzettaufficiale.it/eli/id/1982/11/03/082U0802/sg
- DIRETTIVA DEL CONSIGLIO del 18 dicembre 1984 che modifica la direttiva 80/181/CEE per il ravvicinamento delle legislazioni degli Stati membri relative alle unità di misura.
https://eur-lex.europa.eu/legal-content/IT/TXT/PDF/?uri=CELEX:31985L0001
- DECRETO 29 gennaio 2001. Attuazione della direttiva 1999/103/CE che modifica la direttiva 80/181/CEE sul riavvicinamento delle legislazioni degli Stati membri relative alle unita' di misura. GU Serie Generale n.27 del 02-02-2001
https://www.gazzettaufficiale.it/eli/id/2001/02/02/001A1152/sg
- DECRETO 29 ottobre 2009. Attuazione della direttiva 2009/3/CE del Parlamento europeo e del Consiglio dell'11 marzo 2009 che modifica la direttiva 80/181/CEE del Consiglio sul riavvicinamento delle legislazioni degli Stati membri riguardo alle unita' di misura. (09A13580). GU Serie Generale n.273 del 23-11-2009
https://www.gazzettaufficiale.it/eli/id/2009/11/23/09A13580/sg
- DECRETO 7 aprile 2020. Attuazione della direttiva (UE) 2019/1258 della Commissione del 23 luglio 2019 che modifica, ai fini dell'adattamento al progresso tecnico, l'allegato della direttiva 80/181/CEE del Consiglio per quanto riguarda le definizioni delle unita' SI di base.
https://www.gazzettaufficiale.it/eli/id/2020/05/09/20A02529/sg
[2] Tutti i documenti del SI sono in versione bilingue, in francese e in inglese.
Brochure sur le SI: Le Système international d'unités.
https://www.bipm.org/fr/publications/si-brochure
SI Brochure: The International System of Units (SI).
https://www.bipm.org/en/publications/si-brochure
[3] VIM: International Vocabulary of Metrology. Alla pagina: CGM Publications: Guides in Metrology.
https://www.bipm.org/en/committees/jc/jcgm/publications
[4] Nel caso delle scale numeriche la definizione metrologica parla solo di scala di misura e non distingue tra scala numerica continua e scala numerica discreta in quanto quest'ultima viene considerata come caso limite nel quale l'unità di misura è "uno".
[5] S. S. Stevens. On the Theory of Scales of Measurement. Science, New Series, Vol. 103, No. 2684 (Jun. 7, 1946), pp. 677-680. American Association for the Advancement of Science.
http://www.jstor.org/stable/1671815
[6] "FOR SEVEN YEARS A COMMITTEE of the British Association for the Advancement of Science debated the problem of measurement. Appointed in 1932 to represent Section A (Mathematical and Physical Sciences) and Section J (Psychology), the committee was instructed to consider and report upon the possibility of "quantitative estimates of sensory events"-meaning simply: Is it possible to measure human sensation? Deliberation led only to disagreement, mainly about what is meant by the term measurement".
[7] Lo spazio unificatore non cambia ampiezza e non consente di andare a capo, lasciando quindi l'espressione sempre correttamente impaginata. In ambiente Windows può essere inserito tenendo premuti contemporaneamente i tasti <ctrl> e <shift> e premendo la barra spaziatrice, oppure tenendo premuto il tasto <alt> e digitando 255 sul tastierino numerico, su Mac tenendo premuto il tasto <alt> e premendo la barra spaziatrice.
[8] Non è questa la sede per trattare un tema così complesso e delicato, ma un esempio di come la confusione terminologica possa sfociare in confusione concettuale lo si trova in: Paul C. Price, Rajiv S. Jhangiani, I-Chant A. Chiang, Dana C. Leighton, and Carrie Cuttler. Research Methods in Psychology. 3rd American Edition
https://opentext.wsu.edu/carriecuttler/
laddove gli autori si chiedono al punto 4.1 "Cosa è la misura?" rispondendo che in psicologia "La misura è l'assegnazioni di punteggi agli individui..." – secondo loro analogamente a come in fisica il risultato di una procedura per il calcolo dell'energia potenziale di un oggetto "... è un punteggio che rappresenta l'energia potenziale dell'oggetto...". Ma si tratta di una affermazione errata e fuorviante in quanto ignora il fatto che per "rappresentare" l'energia potenziale è necessario che il "punteggio" (ma forse sarebbe meglio chiamarlo "valore numerico" [VIM 1.20]) sia associato indissolubilmente alle sue dimensioni fisiche [VIM 1.7] attraverso una grandezza [VIM 1.4 e 1.5] e le relative unità di misura [VIM 1.9]. Mentre quella che un loro punteggio (score) in psicologia "misura" – se sono loro stessi ad affermare che "... il punto importante qui è che la misurazione non richiede strumenti o procedure particolari. Non è necessario posizionare individui o oggetti sulla bilancia, porre davanti a loro dei regoli graduati o inserire termometri al loro interno. Ciò che richiede è una procedura sistematica per assegnare punteggi a individui o oggetti in modo che tali punteggi rappresentino la caratteristica di interesse" – o è semplicemente una valutazione da esprimere in una scala nominale o al massimo può essere una quantità esprimibile in una scala ordinale (che il VIM al punto 1.26 definisce come una "quantità definita mediante un procedimento di misurazione convenzionale, per la quale può essere stabilita una relazione di ordinamento totale, secondo la grandezza, con altre quantità dello stesso tipo, ma per la quale non esistono operazioni algebriche tra tali quantità").
[9] Argentina, Austria-Ungheria, Belgio, Brasile, Danimarca, Francia, Germania, Italia, Perù, Portogallo, Russia, Spagna, Svezia e Norvegia, Svizzera, Turchia, Stati Uniti, Venezuela.
https://www.bipm.org/en/metre-convention
[10] Arabia Saudita, Argentina, Australia, Austria, Belgio, Bielorussia, Brasile, Bulgaria, Canada, Cile, Cina, Colombia, Costa Rica, Corea (Repubblica), Croazia, Danimarca, Ecuador, Egitto, Emirati Arabi Uniti, Estonia, Finlandia, Francia, Germania, Giappone, Grecia, India, Indonesia, Iran (Repubblica Islamica), Iraq, Irlanda, Israele, Italia, Kazakistan, Kenya, Lituania, Malaysia, Marocco, Messico, Montenegro, Norvegia, Nuova Zelanda, Olanda, Pakistan, Polonia, Portogallo, Regno Unito, Repubblica Ceca, Romania, Russia (Federazione), Serbia, Singapore, Slovacchia, Slovenia, Sudafrica, Spagna, Stati Uniti, Svezia, Svizzera, Thailandia, Tunisia, Turchia, Ucraina, Ungheria, Uruguay.
https://www.bipm.org/en/member-states
[11] Albania, Azerbaijan, Bangladesh, Bolivia, Bosnia-Erzegovina, Botswana, Cambogia, CARICOM (la Comunità caraibica), Etiopia, Georgia, Ghana, Hong Kong (Cina), Giamaica, Kuwait, Latvia, Lussemburgo, Malta, Mauritius, Moldavia (Repubblica), Mongolia, Namibia, Macedonia del Nord, Oman, Panama, Paraguay, Perù, Filippine, Qatar, Siria, Sri Lanka, Taiwan, Tanzania, Uzbekistan, Vietnam, Zambia, Zimbabwe.
https://www.bipm.org/en/associates
[12] Residui di storiche unità non-SI (miglia, acri, galloni, libbre, gradi Fahrenheit) permangono ancora nelle United States Customary Units e nel Sistema Imperiale Britannico, il cui uso è ammesso rispettivamente da USA e Regno Unito accanto al SI ufficialmente adottato.