Gradi centigradi o gradi Celsius?

Se è vero che la statistica è la tecnica che consente di fornire un supporto scientifico alle evidenze fornite dalle misure, ci sono dal punto di vista metodologico, nelle misure da sottoporre ad analisi statistica, quattro aspetti sull'importanza dei quali non mi stancherò mai di richiamare l'attenzione [1], uno dei quali è:

→ l'utilizzo di un sistema di unità di misura razionale, documentato e condiviso quale è il Sistema internazionale di unità (SI) –  adottato per legge anche in Italia – applicandone integralmente e senza eccezioni le indicazioni.

Per l'appunto: il Sistema Internazionale di unità (SI) è stato adottato per legge in Italia nel 1982, e le successive modifiche sono state adottate per legge nel 2001, nel 2009 e nel 2020 [2]. 

Ma perché ricordare una cosa che dovrebbe essere arcinota?

Perché un bel giorno ricevo una mail che contiene, tra le anteprime giornalistiche del quotidiano al quale sono abbonato, questa immagine e il suo commento.

Faccio una rapida ricerca su Google e trovo che se le espressioni "grado celsius" e "gradi celsius" sono citate 737 000 volte, le espressioni "grado centigrado" e "gradi centigradi" sono citate ben 268 000 volte: insomma, più di una volta su quattro viene utilizzata una espressione impropria.

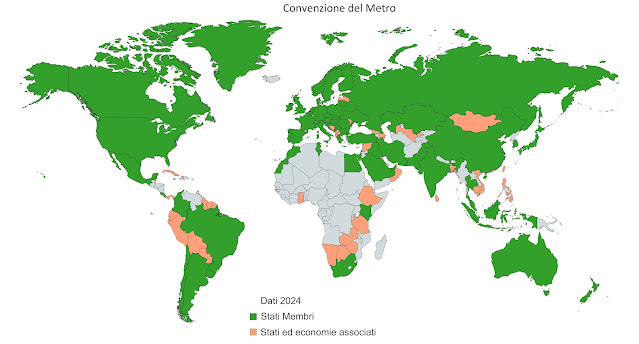
L'Italia ha aderito alla Convenzione del Metro il 20 maggio 1875 adottando il sistema metrico decimale – che successivamente si è evoluto nei sistemi di unità di misura prima MKS (nel 1913), poi MKSA (nel 1954) e infine nell'attuale Sistema Internazionale di Unità (SI) (in Italia adottato per legge dal 1982, e nato ufficialmente nel 1948). 

Ma il Sistema Internazionale di unità (SI) non prevede il grado centigrado! (che è una vecchia espressione, ereditata dal sistema metrico decimale, e oggi superata dalla moderna ridefinizione delle scale di temperatura del SI).

La brochure ufficiale che illustra il SI [3] riporta tra le molte altre cose le sette unità di base del SI, che includono la temperatura termodinamica espressa in kelvin (K):

(a) I simboli delle grandezze sono generalmente singole lettere dell'alfabeto Latino o Greco, sono in carattere corsivo (in francese "italique"; in inglese "italic") e sono raccomandazioni.

(b) I simboli delle unità sono in carattere tondo (in francese "romain"; in inglese "roman") e sono mandatori.

(c) Dopo i simboli non si deve mettere il punto (kg e non kg. ovvero mol e non mol. e così via): si tratta appunto di simboli, e non di abbreviazioni.

Sempre come riportato nella brochure, dalle unità di base del SI si ricavano le ventidue unità SI con nomi e simboli speciali che seguono e che includono la temperatura Celsius espressa in gradi Celsius (°C):

Il valore numerico di una temperatura Celsius (t) espressa in gradi Celsius (°C) è collegato al valore numerico di una temperatura termodinamica (T) espressa in kelvin (K) dalla relazione

t/°C = T/K - 273.15  [4]

Da notare che in questo modo il valore numerico di una differenza (o intervallo) di temperatura è lo stesso quando espresso in kelvin o in gradi Celsius: se una temperatura aumenta (ad esempio) di 10 kelvin, aumenta anche esattamente di 10 gradi Celsius. Mentre posso dire che questa mattina nel giardino di casa il mio termometro segnava "una temperatura di 0 gradi [Celsius]" piuttosto che "una temperatura di 273.15 kelvin". 

Come riportato anche nella SI Brochure [3] la decisione di adottare il Sistema Internazionale di unità (SI) è stata presa durante la 9ª CGPM (la Conferenza Generale dei Pesi e Misure ovvero il "parlamento" nel quale i rappresentanti nazionali discutono e adottano le decisioni in merito alle convenzioni in campo metrologico) che si è tenuta nel 1948. In quella occasione si è anche deciso di adottare – in luogo del fino ad allora denominato "grado centesimale" o "grado centigrado" – il "grado Celsius", in onore dello svedese Anders Celsius che nel 1742 aveva pubblicato, negli Atti della Accademia Reale Svedese di Scienze, la proposta di adottare per la misura della temperatura una scala centesimale con due punti fissi, il punto 0 alla temperatura di ebollizione dell'acqua e il punto 100 alla temperatura di congelamento dell'acqua [5]. 

Fu il fisico francese Jean-Pierre Christin nel 1743 a proporre un termometro a mercurio che scambiava tra loro i valori assegnati ai due punti fissi ponendo a 0 gradi la temperatura di congelamento e a 100 gradi la temperatura di ebollizione dell'acqua come descritto in questo documento [6] a p. 250: "En juillet 1743, il fait connaître au public, par la voie des journaux (Mercure de France, etc., etc.), son thermomètre centigrade à mercure, sous le nom de Thermomètre de Lyon, divisé selon la mesure de la dilatation du mercure..." e alle pp. 259-260: "... le zéro vrai du thermomètre de Celsius marquait l'eau bouillante, tandis que le 100 ͤ degré correspondait à la congélation, ce qui est précisément l'inverse de la graduation lyonnaise".

La stessa scala l'adottò, probabilmente senza sapere del lavoro di Christin, Carlo Linneo tre anni dopo il lavoro del suo connazionale Celsius. Infatti nel suo Hortus upsaliensis del 1745 a p. 23 Linneo riporta in una nota: "Thermometrum nostrum est 0 in puncto congelationis et numerat 100 ad gradus aquæ coquentis" [7].

Nella prima metà del '700 la misura della temperatura era considerata dagli scienziati un obiettivo molto importante, se in precedenza:

→ già nel 1724 il tedesco Daniel Gabriel Fahrenheit, ispirandosi a studi ancora precedenti del danese Ole Christensen Rømer, aveva proposto l'impiego del mercurio e di una scala delle temperature [8] che, dopo varie modifiche, è diventata l'attuale scala Fahrenheit (il grado Fahrenheit, con il simbolo °F, è ammesso per l'uso corrente negli USA, nei quali comunque si impiegano in campo scientifico le unità del SI al quale gli USA aderiscono), che fissa a 32 gradi il punto di congelamento dell'acqua e a 212 gradi il punto di ebollizione, con un intervallo di 180 gradi tra le due temperature;

→ nel 1732 il francese René-Antoine Ferchault de Réaumur aveva proposto un termometro ad alcool con un intervallo di 80 gradi: "Il s'est déterminé à faire remplir les Thermometres d'un Esprit de Vin, dont le volume étant de 1000 parties, lorsqu'il a pris le froid de l'eau qui commence à se geler, devient 1080, lorsqu'il a pris le plus grand degré de chaleur que l'eau puisse lui donner sans le faire boüillir" [9], in un lavoro cui si era ispirato Christin.

Infine non dobbiamo dimenticare i contributi di scienziati italiani in quelli che erano stati i primordi nella misura delle temperature, con:

→ il termoscopio, lo strumento messo a punto da Galileo Galilei nel 1597 che a livello sostanzialmente qualitativo "evidenziava le variazioni della densità dell'aria prodotte dalle variazioni di temperatura" [10];

→ vari tipi di termometro tra cui il termometro a fiala [11] – descritto nel 1666 nei verbali dell'Accademia del Cimento [12] come "... un Termometro ma piu pigro, e infingardo di tutti gli altri. Poichè dove quegli per ogni poco, che l'aria ſi ſtemperi veggonſi ſubito alterare, queſt'altro non è tanto veloce, ed a muoverlo vi vuol'altro che minime, ed inſenſibili differenze. Nulladimeno perchè di queſti ancora, n'è andati in diuverſe parti dentro, e fuori d'Italia; ſi dira brevemente in queſto luogo della loro fabbrica…" – che appartiene alla fase della misura semiquantitativa della temperatura, effettuata in questo caso mediante ampolle colorate che si muovono su e giù al cambiare della densità (che è funzione della temperatura) del mezzo in cui sono immerse. Nell'immagine a destra una versione attuale, impropriamente denominata "termometro galileiano", del termometro a fiala indicato come V nella tavola di sinistra, tratta da [12]: i cinque termometri da I a V illustrati erano riempiti con "il ſottiliſsimo ſpirito del vino, o acquarzente". Come VI nella tavola è indicato invece uno strumento che serviva "per riconoscere le differenze dell'umido nell'aria".

Conclusione: il mio sogno nel cassetto, uno dei tanti? Non vedere mai più temperature riportate in gradi centigradi. Per favore (e per razionalità scientifica, oltre che per una norma vigente) o parliamo di kelvin (K), ma questo avviene in ambito scientifico, o parliamo in alternativa di gradi Celsius (°C), cioè nei termini corretti delle unità di misura della temperatura nelle quali dobbiamo esprimerci [13]. E in ogni caso chiediamo che i dati da elaborare statisticamente siano sempre espressi con le grandezze, le denominazioni, le unità di misura, i simboli, i multipli e i sottomultipli del SI, indirizzando l'interlocutore al bisogno anche alle JCGM Publications: Guides in Metrology [14].

----------

[1] Vedere il post Grandezze e unità di misura SI.

[2] Il Sistema Internazionale di unità (SI) diviene legale in Italia nel 1982, le successive modifiche sono recepite nel 2001, nel 2009 e nel 2020, questa è la normativa aggiornata a inizio 2024, che include la correzione riportata a livello comunitario nel 1984:

- DECRETO DEL PRESIDENTE DELLA REPUBBLICA 12 agosto 1982, n. 802. Attuazione della direttiva (CEE) n. 80/181 relativa alle unita' di misura. GU Serie Generale n.302 del 03-11-1982 - Suppl. Ordinario.

https://www.gazzettaufficiale.it/eli/id/1982/11/03/082U0802/sg

- DIRETTIVA DEL CONSIGLIO del 18 dicembre 1984 che modifica la direttiva 80/181/CEE per il ravvicinamento delle legislazioni degli Stati membri relative alle unità di misura.

https://eur-lex.europa.eu/legal-content/IT/TXT/PDF/?uri=CELEX:31985L0001

- DECRETO 29 gennaio 2001. Attuazione della direttiva 1999/103/CE che modifica la direttiva 80/181/CEE sul riavvicinamento delle legislazioni degli Stati membri relative alle unita' di misura. GU Serie Generale n.27 del 02-02-2001 

https://www.gazzettaufficiale.it/eli/id/2001/02/02/001A1152/sg

- DECRETO 29 ottobre 2009. Attuazione della direttiva 2009/3/CE del Parlamento europeo e del Consiglio dell'11 marzo 2009 che modifica la direttiva 80/181/CEE del Consiglio sul riavvicinamento delle legislazioni degli Stati membri riguardo alle unita' di misura. (09A13580). GU Serie Generale n.273 del 23-11-2009 

https://www.gazzettaufficiale.it/eli/id/2009/11/23/09A13580/sg

- DECRETO 7 aprile 2020. Attuazione della direttiva (UE) 2019/1258 della Commissione del 23 luglio 2019 che modifica, ai fini dell'adattamento al progresso tecnico, l'allegato della direttiva 80/181/CEE del Consiglio per quanto riguarda le definizioni delle unita' SI di base.

https://www.gazzettaufficiale.it/eli/id/2020/05/09/20A02529/sg

[3] SI Brochure: The International System of Units (SI)

https://www.bipm.org/en/publications/si-brochure

[4] La spiegazione della notazione impiegata è riportata nella SI Brochure [3] e a pag. 52 del mio ebook su Grandezze e unità di misura che può essere scaricato a questi link:

https://www.academia.edu/41041923/

https://play.google.com/books/reader?id=GciVDwAAQBAJ

https://www.bayes.it/SI.pdf

[5] Celsius, Anders (1742). Observationer om twänne beständiga grader på en thermometer. Kungliga Svenska Vetenskapsakademiens Handlingar (3): 171–180.

https://archive.org/stream/kungligasvenskav1317kung

[6] SUR L'INVENTION DU THERMOMÈTRE CENTIGRADE A MERCURE, Faite à Lyon par M. CHRISTIN. NOTICE LUE A LA SOCIÉTÉ D'AGRICULTURE DE LYON, Dans la séance du 4 juillet 1845. In: ANNALES DES SCIENCES PHYSIQUES ET NATURELLES, D'AGRICULTURE ET D'INDUSTRIE, PUBLIÉES PAR La Société royale d'Agriculture, etc., DE LYON. TOME VIII. 1845.

https://play.google.com/books/reader?id=o4g9AQAAMAAJ

[7] Hortus upsaliensis, 1745.

https://ia800503.us.archive.org/16/items/naucler-1745/Naucler1745.pdf

[8] VIII. Experimenta & observationes de congelatione aquæ in vacuo factæ a D. G. Fahrenheit, R. S. S. In: Philosophical Transactions of the Royal Society of London, Volume 33, Issue 382. Published: 30 April 1724.

https://doi.org/10.1098/rstl.1724.0016

[9] Explication des principes établis par M. de Reaumur, pour la construction des thermometres dont les degrés soient comparables. 1732.

https://gallica.bnf.fr/ark:/12148/bpt6k6535672b/

[10] Museo Galileo. Termoscopio.

https://catalogo.museogalileo.it/oggetto/Termoscopio.html

[11] Museo Galileo. Termometri a fiala.

https://catalogo.museogalileo.it/oggetto/TermometriFiala.html

[12] DI NATVRALI ESPERIENZE FATTE NELL'ACCADEMIA DEL CIMENTO SOTTO LA PROTEZIONE DEL SERENISSIMO PRINCIPE LEOPOLDO DI TOSCANA E DESCRITTE DAL SEGRETARIO DI ESSA ACCADEMIA. IN FIRENZE. MDCLXVI. 

https://play.google.com/books/reader?id=BcCpGiXkRKsC

[13] Notare tra l'altro che, poiché la legge non ammette ignoranza, un atto legale che riporta una temperatura espressa in "gradi centigradi" potrebbe essere impugnato.

[14] Vedere i documenti:

– GUM: Guide to the Expression of Uncertainty in Measurement

– VIM: International Vocabulary of Metrology

https://www.bipm.org/en/committees/jc/jcgm/publications

Multipli e sottomultipli delle unità di misura SI

Statistica significa analisi dei dati, cioè dei risultati di processi di misura espressi in termini di grandezze, di unità di misura e dei loro multipli e sottomultipli. 

Ho riportato altrove [1] la storia che dalle antiche misure antropomorfe, attraverso la svolta che è seguita alla nascita della scienza moderna, ha condotto anche l'Italia a riconoscere la necessità di adottare un linguaggio delle misure rigoroso e ampiamente concordato e condiviso a livello scientifico, oltre che in grado di risolvere le esigenze pratiche quotidiane, prima con l'adesione nel 1875 al Sistema metrico decimale e successivamente adottando per legge nel 1982  il Sistema internazionale di unità (SI) che ne rappresenta la moderna evoluzione [2].

Così come si trova citato anche nella Appendice 1 della Brochure del SI [3], nel 2022 la 27a CGPM [4] con una delle sue risoluzioni [5] ha aggiunto, ai precedenti, due altri multipli (ronna e quetta) e due altri sottomultipli (ronto e quecto), quindi per indicare multipli e sottomultipli delle unità di misura nel SI sono ad oggi previsti i prefissi, i simboli e i corrispondenti fattori di moltiplicazione riportati in questa tabella:

Lo scopo è evidente: se il numero di cifre diventa eccessivo e si trova ostica per l'uso corrente e non si vuole impiegare la notazione scientifica [6], ma si preferisce esprimere in forma verbale i numeri superiori al milione, i prefissi SI consentono di evitare la trappola delle denominazioni che in tutta Europa con la scala lunga [7], e negli USA e in molti altri Paesi con la scala corta, prevedono di impiegare gli stessi termini per indicare numeri completamente diversi, come qui evidenziato,

un fatto che determina confusione e possibili errori nella interpretazione dei numeri espressi in forma verbale quando questi sono riportati da una lingua all'altra [8].

Pertanto – giusto per fare un esempio – per la constatazione che "... as of April 2024 Apple has a market cap of $2.547 Trillion..." [9] è opportuno precisare che i 2.547 trilioni di dollari di capitalizzazione dell'Apple sono espressi nella scala corta dei Paesi anglosassoni, e quindi sono 2.547 ∙ 10¹² dollari, e non sono i 2.547 ∙ 10¹⁸ dollari corrispondenti ai trilioni della scala lunga.

Invece nessun dubbio vi può essere nel caso della larghezza di banda espressa in bit (b) di una rete a 100 Mb/s (100 megabit al secondo ovvero 100 ∙ 10⁶ bit al secondo) e della capacità espressa in byte (B) di una RAM di 16 GB (16 gigabyte ovvero 16 ∙ 10⁹ byte) o di un hard-disk di 4 TB (4 terabyte ovvero 4 ∙ 10¹² byte), dato il significato univoco dei prefissi SI.  

----------

[1] Grandezze e unità di misura. Breve storia dall'antichità al Sistema Internazionale di Unità (SI). Vedere il post:

https://impararfacendo.blogspot.com/2020/10/grandezze-e-unita-di-misura.html

Il testo può essere liberamente scaricato (e senza pubblicità diretta nè occulta) da questi siti

https://www.academia.edu/41041923/

https://books.google.it/books?id=GciVDwAAQBAJ

come pure dal mio sito personale

https://www.bayes.it/SI.pdf

[2] I riferimenti normativi completi altre che nel testo citato sono riportati  nel  post Scale nominali, scale ordinali e scale numeriche.

[3] SI Brochure: The International System of Units (SI) – 9a edizione, 2019.

https://www.bipm.org/en/publications/si-brochure

[4] Sigla della "Conferenza Generale dei Pesi e delle Misure", in sostanza il parlamento attraverso il quale si esprimono in tema di misure gli Stati che hanno adottato il SI.

[5] Vedere: Resolution 3 of the 27th CGPM (2022). On the extension of the range of SI prefixes. The General Conference on Weights and Measures (CGPM), at its 27th meeting.

https://www.bipm.org/en/cgpm-2022/resolution-3

[6] Vedere il post Come riportare i numeri in formato fisso.

[7] La scala lunga la si trova riportata anche in Italia nella legislazione, come ad esempio nella tabella a pagina 12 dell'Allegato al DECRETO MINISTERIALE 4 settembre 1996 Attuazione della direttiva 94/55/CE del Consiglio concernente il ravvicinamento delle legislazioni degli Stati membri relative al trasporto di merci pericolose su strada. (GU Serie Generale n.282 del 02-12-1996 - Suppl. Ordinario n. 211).

[8] Vedere: Long and short scales. 

https://en.wikipedia.org/wiki/Long_and_short_scales

 

[9] Dati tratti da: Largest Companies by Market Cap

https://companiesmarketcap.com/

Scale nominali, scale ordinali e scale numeriche

Le relazioni che intercorrono tra il tipo di variabile, il processo mediante il quale viene ottenuto il dato, la modalità di espressione del dato e il tipo di scala nella quale il dato viene espresso forniscono la definizione operativa delle scale di misura.

Questa definizione deriva dalla loro definizione metrologica prevista nel Sistema internazionale di unità (SI), che l'Italia nel 1982 ha adottato per legge, aggiornandolo successivamente con le modifiche via via apportate [1].

Le generalità del SI sono riportate nella brochure pubblicata dal Bureau international des poids et mesures (BIPM) [2] mentre il glossario del processo di misura è riportato nel VIM, il Vocabolario Internazionale di Metrologia [3], nel quale le scale di misura sono così definite:
→ scala di riferimento convenzionale – scala di valori definita mediante un accordo ufficiale [VIM 1.29]
→ scala ordinale – scala di valori per una grandezza ordinale [VIM 1.28]
→ scala di valori o scala di misura – insieme ordinato dei valori di grandezze di una data natura, utilizzato per classificare le grandezze di quella natura in ordine crescente o decrescente in base alle loro espressioni quantitative [VIM 1.27]

Quindi la definizione operativa delle scale di misura, a parte semplificare, ma senza cambiarne il senso, la definizione della "scala di riferimento convenzionale" riportandola da un "accordo ufficiale" al caso delle meno burocratiche, universalmente impiegate e più immediatamente intuitive scale nominali, riprende tal quale la definizione delle scale ordinali e semplicemente suddivide le scale numeriche, lasciandone immodificata la definizione metrologica riportata dal VIM, in discrete e in continue in base al processo mediante il quale è ottenuto il dato: conteggio o misura [4]. Questa suddivisione trova ulteriore supporto nel fatto che il processo di conteggio fornisce risultati espressi sotto forma di numeri interi e di una sola unità di misura (“uno”) basata sulla grandezza “numero di entità” che non ha dimensioni [VIM 1.4 e 1.8], mentre il processo di misura fornisce risultati espressi sotto forma di numeri razionali e di differenti unità di misura (metro, secondo, kilogrammo, eccetera) basate su grandezze (lunghezza, tempo, massa e quant’altro) che hanno una dimensione fisica [VIM 1.7]. 

Ma a questo punto la domanda è inevitabile: se esistono definizioni ufficiali, ampiamente condivise e addirittura normate, dalle quali è possibile trarre una definizione operativa piuttosto chiara che le collega ai processi di misura impiegati nella pratica, perché si trova riportato quasi dappertutto che le scale di misura sono classificate in: scale nominali, scale ordinali, scale a intervalli, scale a rapporti ?

La risposta è: per qualche ragione imperscrutabile, probabilmente potenziata dalla disponibilità del copia-e-incolla, un meme è riuscito a moltiplicarsi in modo virale fino ad occupare quasi completamente l'infosfera concernente questo argomento. E senza ragione, senza un razionale.

La proposta di suddivisione in scale nominali, scale ordinali, scale a intervalli, scale a rapporti è riportata in un lavoro del 1946 di S. S. Stevens [5], che proprio all'inizio del lavoro scrive: "PER SETTE ANNI UN COMITATO dell'Associazione britannica per l'avanzamento della scienza ha dibattuto il problema della misurazione. Nominato nel 1932 a rappresentare la Sezione A (Matematica e scienze fisiche) e Sezione J (Psicologia), il comitato è stato incaricato di considerare e riferire sulla possibilità di "stime quantitative di eventi sensoriali", che significano semplicemente: è possibile misurare le sensazioni umane? La riflessione ha portato solo al disaccordo, soprattutto su cosa si intende con il termine misurazione" [6].

La domanda che Stevens si pone "è possibile misurare le sensazioni umane?" sarà pure lecita, ma non si possono avere dubbi "su cosa si intende con il termine misurazione". 

Una misurazione o procedimento di misura consiste nell'esprimere una grandezza in modo quantitativo, mediante un "valore numerico" che è un numero puro uguale al rapporto tra il "(valore della) grandezza (in esame)" e il valore di una grandezza di riferimento ad essa omogenea definita come "unità di misura", ed è quindi 

(valore della) grandezza (in esame) / unità di misura = valore numerico

Corollario: il risultato di una misura ovvero il "(valore della) grandezza (in esame)" è dato dal prodotto di un "valore numerico" per la "unità di misura"

(valore della) grandezza (in esame) = valore numerico · unità di misura

Per indicare il prodotto, rendendo "valore numerico" e "unità di misura" un tutt'uno inscindibile, il simbolo del prodotto [ · ] per convenzione viene sostituito con lo spazio unificatore [7], come avviene ad esempio in 2.5 m, 12 s, 75 kg (unica eccezione sono le unità angolari, per le quali lo spazio tra il valore numerico e il simbolo dell'unità non è previsto, pertanto un angolo verrà riportato, ad esempio, come 41°54'39).

Il lavoro di Stevens è viziato da un errore concettuale di fondo: nel tentativo di "misurare le sensazioni umane" e dare dignità di "misura" ai risultati dei metodi di ricerca in psicologia, ha cercato di adattare alla psicologia "... il termine misurazione..." – che ha e deve avere una definizione univoca – pensando di risolvere il problema con nuove definizioni delle scale di misura, mentre avrebbe dovuto ricercare la "... possibilità di "stime quantitative di eventi sensoriali"..." in una qualche grandezza [VIM 1.1] e nella sua unità di misura [VIM 1.9], perché senza il fondamento di grandezze [misurabili] e delle loro unità di misura, le scale di misura [VIM 1.27] sono una espressione vuota.

Quindi mentre per misura [VIM 2.1] e per tutti gli altri termini che devono essere impiegati per esprimersi correttamente in campo scientifico (ma anche nella vita di tutti i giorni) rimando al SI e alle definizioni del VIM, qui mi limito a rilevare che la forzatura impiegata da Stevens per accreditare le misure in campo psicologico ha determinato solamente confusione terminologica, anticamera della confusione concettuale [8].

Se proprio si vuole ricollegare la definizione di Stevens delle scale di misura – inutile dire che è fortemente sconsigliata anche in campo psicologico, al quale nulla aggiunge rispetto alle scale ufficiali qui trattate: in ogni caso il VIM semplicemente la ignora – alla definizione operativa delle scale di misura in campo scientifico, e con questa alla loro definizione metrologica, basta notare che:

- se i dati sono espressi in una scala numerica discreta possiamo avere: 

[A] quella che Stevens denomina scala a intervalli quando, come accade ad esempio per le date, non sono possibili rapporti (non posso dividere il 28 febbraio per il 2 febbraio) ma posso solamente calcolare l'intervallo che le separa (nel caso specifico 26 giorni); 

[B] quella che Stevens denomina scala a rapporti quando, come accade ad esempio per il numero di auto ferme al semaforo, se prima ne ho contate 5 e dopo ne ho contate 4, oltre a calcolare la differenza posso calcolare anche il rapporto prima-dopo che è 1.25;

- se i dati sono espressi in una scala numerica continua possiamo avere:

[A] quella che Stevens denomina scala a intervalli quando, come accade ad esempio per la temperatura in gradi Celsius (°C), posso dire che tra la temperatura di +20 °C e la temperatura di -10 °C c'è un intervallo di 30 °C, ma non posso dividere la prima per la seconda;

[B] quella che Stevens denomina scala a rapporti quando, come accade ad esempio per la concentrazione del colesterolo nel siero, posso calcolare non solo l'intervallo tra due valori (la mia concentrazione di colesterolo è 220 mg/dL, la tua 110 mg dL, la differenza è di 110 mg/dL) ma anche il rapporto (la mia concentrazione del colesterolo è 2.0 volte la tua).

Questo significa che (tolte le scale nominali e le scale ordinali sulle quali tutti concordano) quelle di Stevens non sono scale di misura ma, nella migliore e proprio nella migliore delle ipotesi, potrebbero (e uso il condizionale) essere considerate un attributo aggiuntivo (ma privo di interesse metrologico) delle scale numeriche. Riprendiamo quindi la nostra definizione operativa delle scale di misura, che trova un fondamento nel SI e nel VIM e che fornisce il razionale su cui si fondano le modalità di rappresentazione grafica e di analisi statistica dei dati.

Il tipo più semplice di scala è rappresentato dalla scala nominale. Corrisponde ai dati della natura più elementare, quella di dati qualitativi per i quali è disponibile solamente una descrizione verbale. Ne sono un esempio la classificazione maschio / femmina, la classificazione dei gruppi sanguigni ABO (O, A, B, AB), dei motori (endotermici, esotermici, elettrici, eccetera), delle specie animali (ad esempio: cane domestico, sciacallo, coyote, lupo, dingo) e così via. La misura più intuitiva e più utilizzata, nel caso della scala nominale, è costituita dalla percentuale (o dalla proporzione o frazione). In questo caso le rappresentazioni che si possono impiegare sono il grafico a torta (pie-chart) e, quando le grandezze da rappresentare sono indipendenti e non costituiscono la parte di un tutto, il grafico a barre (barplot) con le barre staccate e disposte orizzontalmente.

Nel caso di dati qualitativi per i quali è disponibile una descrizione sotto forma di attributo ordinabile si ha a che fare con una scala ordinale. Questo avviene per esempio per la classificazione in neonati, bambini e adulti, nella quale è appropriato applicare un ordinamento crescente per classi di età (neonato < bambino < adulto), per il livello di scolarità (scuola elementare < scuola media < diploma < laurea), eccetera. Un altro esempio è la classificazione per ranghi, nella quale il valore osservato viene trasformato nel corrispondente rango, cioè nel numero della posizione che il dato occupa nella lista ordinata dei dati. Così la classificazione inadeguato / parzialmente adeguato / adeguato / più che adeguato / eccellente può essere trasformata nella classificazione 1 / 2 / 3 / 4 / 5. Per le scale ordinali è possibile utilizzare un grafico a torta (pie-chart) oppure, per valorizzare la possibilità di ordinamento delle classi, un grafico a barre (barplot) con le barre staccate per indicare la discontinuità.

Una scala numerica discreta è tipicamente quella relativa a dati numerici ottenuti mediante operazioni di conteggio e riportati sotto forma di interi o numeri naturali (1, 2, 3, ….). Si prenda ad esempio il conteggio degli eritrociti (globuli rossi) nel sangue. La differenza minima tra due conteggi teoricamente misurabile è rappresentata da un globulo rosso: i dati sono numerici, ma tra l'uno l'altro non esistono valori intermedi. Altri esempi di scala numerica discreta sono il numero di controlli medici effettuati da una donna durante la gravidanza, il numero di insegnanti di ruolo nel liceo vicino a casa, il numero di auto ferme al semaforo e così via. Per le scale numeriche discrete si possono utilizzare un grafico a barre (barplot) con le barre staccate per indicare la discontinuità ma non l'istogramma che è basato sull'ipotesi di continuità dei dati, o anche, nel caso in cui si debbano rappresentare contemporaneamente due variabili, un grafico di dispersione (grafico xy o grafico cartesiano o scatterplot) precisando che i valori compresi tra due interi non hanno un corrispettivo reale.

La scala numerica continua è tipicamente quella impiegata per rappresentare dati numerici ottenuti mediante procedimenti di misura come quelli chimici e quelli fisici e i cui dati sono riportati sotto forma di numeri razionali (1.435, 123.9, 84.327, ...). Esempi ne sono la misura della concentrazione del colesterolo nel sangue, la misura della distanza tra due luoghi, la misura della velocità di un'auto, la misura del peso di una persona e quant'altro. L'intervallo tra due valori può essere suddiviso a piacere, anche se non oltre i limiti del potere di risoluzione degli strumenti di misura, che impongono nella pratica un numero molto limitato di cifre significative. Per le scale numeriche continue è possibile impiegare di volta in volta il classico istogramma, un grafico a linee spezzate come un poligono di frequenza, o ancora un grafico di dispersione (grafico xy o grafico cartesiano o scatterplot) nel caso in cui si debbano rappresentare contemporaneamente due variabili.

Dal punto di vista della statistica, ai dati espressi in forma di scale nominali sono applicabili i test basati sulla enumerazione dei casi (come test chi-quadrato, test di Fisher, test di McNemar), ai dati espressi in forma di scale ordinali sono applicabili in aggiunta i test basati sui ranghi, mentre ai dati espressi in forma di scale numeriche sono applicabili, con la necessaria appropriatezza e le dovute attenzioni, i test basati sulle ipotesi di continuità e gaussianità delle distribuzioni (test parametrici), i test non parametrici e i test basati su modelli bayesiani.

La conclusione? Molto semplice. Siglata per la prima volta a Parigi il 20 maggio 1875 da 17 Stati [9] la Convenzione del metro, che originariamente prevedeva l'impiego del Sistema metrico decimale che si è poi evoluto nel Sistema internazionale di unità, secondo i dati ufficiali forniti dal BIPM all'inizio del 2024 contava 64 Stati Membri [10] e 36 Stati ed economie associati [11].

Considerato che tutte le nazioni più popolose, incluse Cina e India, vi aderiscono, il SI con le sue grandezze e unità di misura è diventato un comune denominatore e un riferimento per miliardi di persone, nella scienza ma anche nella vita quotidiana [12]. 

Tra i documenti che il SI mette a disposizione perché ci si possa avvicinare in modo adeguato al mondo delle misure, il Vocabolario Internazionale di Metrologia riveste un ruolo cruciale: e questo post vuole essere un invito a consultarlo per formare, per informare, per adeguare i nostri modi di riportare i dati ed esprimerci con la necessaria appropriatezza quando parliamo di misure.

Nota bene: in R il separatore delle cifre decimali è il punto (.) e come già riportato altrove questa convenzione per ragioni di omogeneità viene adottata negli script, nei file di dati e nel testo dei post.

----------

[1] Il Sistema Internazionale di unità (SI) diviene legale in Italia nel 1982, le successive modifiche sono recepite nel 2001, nel 2009 e nel 2020, questa è la normativa aggiornata a inizio 2024, che include la correzione riportata a livello comunitario nel 1984:

- DECRETO DEL PRESIDENTE DELLA REPUBBLICA 12 agosto 1982, n. 802. Attuazione della direttiva (CEE) n. 80/181 relativa alle unita' di misura. GU Serie Generale n.302 del 03-11-1982 - Suppl. Ordinario.

https://www.gazzettaufficiale.it/eli/id/1982/11/03/082U0802/sg

- DIRETTIVA DEL CONSIGLIO del 18 dicembre 1984 che modifica la direttiva 80/181/CEE per il ravvicinamento delle legislazioni degli Stati membri relative alle unità di misura.

https://eur-lex.europa.eu/legal-content/IT/TXT/PDF/?uri=CELEX:31985L0001

- DECRETO 29 gennaio 2001. Attuazione della direttiva 1999/103/CE che modifica la direttiva 80/181/CEE sul riavvicinamento delle legislazioni degli Stati membri relative alle unita' di misura. GU Serie Generale n.27 del 02-02-2001 

https://www.gazzettaufficiale.it/eli/id/2001/02/02/001A1152/sg

- DECRETO 29 ottobre 2009. Attuazione della direttiva 2009/3/CE del Parlamento europeo e del Consiglio dell'11 marzo 2009 che modifica la direttiva 80/181/CEE del Consiglio sul riavvicinamento delle legislazioni degli Stati membri riguardo alle unita' di misura. (09A13580). GU Serie Generale n.273 del 23-11-2009 

https://www.gazzettaufficiale.it/eli/id/2009/11/23/09A13580/sg

- DECRETO 7 aprile 2020. Attuazione della direttiva (UE) 2019/1258 della Commissione del 23 luglio 2019 che modifica, ai fini dell'adattamento al progresso tecnico, l'allegato della direttiva 80/181/CEE del Consiglio per quanto riguarda le definizioni delle unita' SI di base.

https://www.gazzettaufficiale.it/eli/id/2020/05/09/20A02529/sg

[2] Tutti i documenti del SI sono in versione bilingue, in francese e in inglese.

Brochure sur le SI: Le Système international d'unités.

https://www.bipm.org/fr/publications/si-brochure

SI Brochure: The International System of Units (SI).

https://www.bipm.org/en/publications/si-brochure

[3] VIM: International Vocabulary of Metrology. Alla pagina: CGM Publications: Guides in Metrology.

https://www.bipm.org/en/committees/jc/jcgm/publications

[4] Nel caso delle scale numeriche la definizione metrologica parla solo di scala di misura e non distingue tra scala numerica continua e scala numerica discreta in quanto quest'ultima viene considerata come caso limite nel quale l'unità di misura è "uno".

[5] S. S. Stevens. On the Theory of Scales of Measurement. Science, New Series, Vol. 103, No. 2684 (Jun. 7, 1946), pp. 677-680. American Association for the Advancement of Science. 

http://www.jstor.org/stable/1671815

[6] "FOR SEVEN YEARS A COMMITTEE of the British Association for the Advancement of Science debated the problem of measurement. Appointed in 1932 to represent Section A (Mathematical and Physical Sciences) and Section J (Psychology), the committee was instructed to consider and report upon the possibility of "quantitative estimates of sensory events"-meaning simply: Is it possible to measure human sensation? Deliberation led only to disagreement, mainly about what is meant by the term measurement".

[7] Lo spazio unificatore non cambia ampiezza e non consente di andare a capo, lasciando quindi l'espressione sempre correttamente impaginata. In ambiente Windows può essere inserito tenendo premuti contemporaneamente i tasti <ctrl> e <shift> e premendo la barra spaziatrice, oppure tenendo premuto il tasto <alt> e digitando 255 sul tastierino numerico, su Mac tenendo premuto il tasto <alt> e premendo la barra spaziatrice.

[8] Non è questa la sede per trattare un tema così complesso e delicato, ma un esempio di come la confusione terminologica possa sfociare in confusione concettuale lo si trova in: Paul C. Price, Rajiv S. Jhangiani, I-Chant A. Chiang, Dana C. Leighton, and Carrie Cuttler. Research Methods in Psychology. 3rd American Edition

https://opentext.wsu.edu/carriecuttler/

laddove gli autori si chiedono al punto 4.1 "Cosa è la misura?" rispondendo che in psicologia "La misura è l'assegnazioni di punteggi agli individui..." – secondo loro analogamente a come in fisica il risultato di una procedura per il calcolo dell'energia potenziale di un oggetto "... è un punteggio che rappresenta l'energia potenziale dell'oggetto...". Ma si tratta di una affermazione errata e fuorviante in quanto ignora il fatto che per "rappresentare" l'energia potenziale è necessario che il "punteggio" (ma forse sarebbe meglio chiamarlo "valore numerico" [VIM 1.20]) sia associato indissolubilmente alle sue dimensioni fisiche [VIM 1.7] attraverso una grandezza [VIM 1.4 e 1.5] e le relative unità di misura [VIM 1.9]. Mentre quella che un loro punteggio (score) in psicologia "misura" – se sono loro stessi ad affermare che "... il punto importante qui è che la misurazione non richiede strumenti o procedure particolari. Non è necessario posizionare individui o oggetti sulla bilancia, porre davanti a loro dei regoli graduati o inserire termometri al loro interno. Ciò che richiede è una procedura sistematica per assegnare punteggi a individui o oggetti in modo che tali punteggi rappresentino la caratteristica di interesse" – o è semplicemente una valutazione da esprimere in una scala nominale o al massimo può essere una quantità esprimibile in una scala ordinale (che il VIM al punto 1.26 definisce come una "quantità definita mediante un procedimento di misurazione convenzionale, per la quale può essere stabilita una relazione di ordinamento totale, secondo la grandezza, con altre quantità dello stesso tipo, ma per la quale non esistono operazioni algebriche tra tali quantità").

[9] Argentina, Austria-Ungheria, Belgio, Brasile, Danimarca, Francia, Germania, Italia, Perù, Portogallo, Russia, Spagna, Svezia e Norvegia, Svizzera, Turchia, Stati Uniti, Venezuela. 

https://www.bipm.org/en/metre-convention

[10] Arabia Saudita, Argentina, Australia, Austria, Belgio, Bielorussia, Brasile, Bulgaria, Canada, Cile, Cina, Colombia, Costa Rica, Corea (Repubblica), Croazia, Danimarca, Ecuador, Egitto, Emirati Arabi Uniti, Estonia, Finlandia, Francia, Germania, Giappone, Grecia, India, Indonesia, Iran (Repubblica Islamica), Iraq, Irlanda, Israele, Italia, Kazakistan, Kenya, Lituania, Malaysia, Marocco, Messico, Montenegro, Norvegia, Nuova Zelanda, Olanda, Pakistan, Polonia, Portogallo, Regno Unito, Repubblica Ceca, Romania, Russia (Federazione), Serbia, Singapore, Slovacchia, Slovenia, Sudafrica, Spagna, Stati Uniti, Svezia, Svizzera, Thailandia, Tunisia, Turchia, Ucraina, Ungheria, Uruguay.

https://www.bipm.org/en/member-states

[11] Albania, Azerbaijan, Bangladesh, Bolivia, Bosnia-Erzegovina, Botswana, Cambogia, CARICOM (la Comunità caraibica), Etiopia, Georgia, Ghana, Hong Kong (Cina), Giamaica, Kuwait, Latvia, Lussemburgo, Malta, Mauritius, Moldavia (Repubblica), Mongolia, Namibia, Macedonia del Nord, Oman, Panama, Paraguay, Perù, Filippine, Qatar, Siria, Sri Lanka, Taiwan, Tanzania, Uzbekistan, Vietnam, Zambia, Zimbabwe. 

https://www.bipm.org/en/associates

[12] Residui di storiche unità non-SI (miglia, acri, galloni, libbre, gradi Fahrenheit) permangono ancora nelle United States Customary Units e nel Sistema Imperiale Britannico, il cui uso è ammesso rispettivamente da USA e Regno Unito accanto al SI ufficialmente adottato.

Come separare i decimali e come raggruppare le cifre

Nel mondo anglosassone 3.142 è un numero con tre cifre decimali, mentre 302,073 sta per trecentoduemilasettantatre.

In Italia e in genere in Europa il primo, il valore (arrotondato) di pi greco (π), si scrive 3,142 mentre il secondo, la superficie dell'Italia espressa in km², si trova sovente riportato, anche in fonti ufficiali, come 302.073 [1].

Assumendo che il lettore, europeo o anglofono, non sappia di avere a che fare con pi-greco e con la superficie dell'Italia, quindi che interpreti il valore numerico alla luce della sola informazione derivante dal proprio contesto linguistico, il significato attribuito a questi numeri è il seguente:

	Significato in relazione al contesto linguistico
	anglosassone	europeo
3,142	Tremila ...	Tre virgola ...
3.142	Tre virgola...	Tremila...
302,073	Trecentoduemila ...	Trecentodue virgola ...
302.073	Trecentodue virgola ...	Trecentoduemila ...

Il significato del punto (.) e della virgola (,) dipende dal contesto linguistico a causa del fatto che sono entrambi usati, a livello internazionale, sia come separatori decimali sia come simboli per il raggruppamento delle cifre. Ma si tratta di una prassi errata.

Perché? 

Perché l'Italia ha aderito alla Convenzione del Metro il 20 maggio 1875 adottando il sistema metrico decimale – che successivamente si è evoluto nei sistemi di unità di misura denominati prima MKS (nel 1913) e poi MKSA (nel 1954) – e ha nel 1982 adottato per legge [2] il loro moderno erede, il Sistema Internazionale di Unità (SI) così battezzato ufficialmente nel 1960 [3, 4]. 

E perché nella XXII Conferenza Generale dei Pesi e delle Misure del 2003, nella risoluzione 10, la CGPM – in sostanza il Parlamento dei Paesi che come l'Italia aderiscono alla Convenzione del Metro [5] – ha stabilito che:

→ "il simbolo per il marcatore decimale deve essere il punto sulla linea [di base] o la virgola sulla linea [di base]", ammettendo quindi, per ragioni pratiche/linguistiche, la coesistenza di questi due simboli;

→ "i numeri possono essere suddivisi in gruppi di tre per facilitare la lettura; [ma] né punti né virgole devono essere inseriti negli spazi tra i gruppi, come stabilito nella risoluzione 7 della IX CGPM, 1948".

Le regole dettate dalla CGPM, concordate addirittura nel lontano 1948, sono quindi molto semplici:

→ per separare i decimali devono essere impiegati o il punto (.) o la virgola (,) liberamente, in modo consono all'uso che si è andato consolidando nel tempo e al contesto linguistico e culturale;

→ raggruppare le cifre è facoltativo ma, nel caso in cui lo si faccia per rendere più agevole la lettura, può essere impiegato esclusivamente lo spazio, visto che per definizione "... né punti né virgole devono essere inseriti negli spazi tra i gruppi...".

Questo cambia tutto, perché se fossero applicate queste semplici regole allora il punto (.) e la virgola (,) sarebbero sempre correttamente intesi per quello che sono, cioè entrambi, per definizione, come separatori dei decimali e mai come simboli per il raggruppamento delle cifre, e la situazione diventerebbe questa:

	Significato in relazione al contesto linguistico
	anglosassone	europeo
3,142 o 3.142	Tre virgola ...	Tre virgola ...
302 073	Trecentoduemila...	Trecentoduemila...
302,073	Trecentoduemila ...	Trecentodue virgola ...
302.073	Trecentodue virgola ...	Trecentoduemila ...

Alla luce di queste regole un anglosassone che leggesse un 3,142 lo interpreterebbe per definizione alla stessa stregua di un 3.142 e un europeo che leggesse un 3.142 lo interpreterebbe alla stessa stregua di un 3,142. A fronte di una diversa scelta nell'impiego del separatore dei decimali (ma “de gustibus non disputandum est”) l'interpretazione sarebbe univoca. E ovviamente nessun dubbio potrebbe mai sorgere nella lettura del 302 073 come trecentoduemilasettantatre.

Qualcuno potrebbe far notare che volendo impiegare lo spazio per raggruppare le cifre rimangono comunque da risolvere due problemi legati al comportamento dei programmi di videoscrittura, che:

→ nel caso in cui si impiega la giustificazione del testo, ampliano e riducono automaticamente gli spazi vuoti ai fini della miglior composizione della riga;

→ potrebbero andare a capo, passando alla riga successiva, proprio a livello dello spazio che separa un gruppo di cifre da quello che lo segue.

Ma questi due problemi sono già stati risolti. Oggi qualsiasi programma di videoscrittura consente di impiegare, oltre allo spazio normale, che si inserisce in un testo con la barra spaziatrice, anche il carattere spazio unificatore: questo spazio non cambia ampiezza e non consente di andare a capo, lasciando quindi il testo che lo include sempre correttamente impaginato.

Lo spazio unificatore, che nella codifica Unicode è denominato NO-BREAK SPACE (NBSP) e ha il codice U+00A0 [6]:

→ su Windows può essere inserito tenendo premuti contemporaneamente i tasti <ctrl> e <shift> e premendo la barra spaziatrice, oppure tenendo premuto il tasto <alt> e digitando 255 sul tastierino numerico;

→ su Mac può essere inserito tenendo premuto il tasto <alt> e premendo la barra spaziatrice;

→ su Linux può essere inserito tenendo premuti contemporaneamente i tasti <ctrl> e <shift> e premendo la barra spaziatrice o tenendo premuto il tasto <shift> e premendo la barra spaziatrice o ricorrendo a una apposita configurazione.

Per separare i decimali R impiega di default e al proprio interno esclusivamente il punto (.) ma permette di importare e di esportare i dati impiegando come separatore dei decimali sia il punto (.) sia la virgola (,) [7].

Se dovete preparare un documento nel quale i numeri (e.g.: 16 miliardi di bit) sono riportati utilizzando la notazione scientifica di default in R (e.g.: 16e+09 bit), o utilizzando i multipli e sottomultipli del SI (e.g.: 16 gigabit) [8], il problema dello spazio unificatore non si pone. Ma se volete esprimere i numeri in formato fisso (e.g.: 16 000 000 000 bit) [9] ricordate che:

→  per facilitarne la lettura i numeri superiori a 999 possono [facoltativamente] essere suddivisi in gruppi di tre cifre [ma esclusivamente] impiegando lo spazio [unificatore].

E c'è pure un altro problema: attualmente in Italia i fogli elettronici, in barba alla razionalità e all'ufficialità dell'approccio definito dalla CGPM, impiegano di default il punto per raggruppare le cifre. Gli utilizzatori si adeguano (difficile che qualcuno si prenda la briga di andare a riconfigurare le opzioni di formattazione dei numeri) e questo induce a perpetuare una errata modalità di rappresentazione.

Conclusione: temo che sarà necessario attendere ancora prima di vedere universalmente e senza eccezione alcuna adottata la prassi corretta che prevede di:

→  separare i decimali impiegando indifferentemente il punto o la virgola (la scelta dipenderà dal contesto linguistico/culturale) con la certezza che i due si equivalgono e che all'interno dei numeri non sono impiegati in altro modo;

→  raggruppare le cifre (al bisogno) impiegando esclusivamente lo spazio unificatore.

Ma sarebbe il classico uovo di Colombo, in quanto queste regole consentono di semplificare, eliminare tutti i potenziali errori di interpretazione e garantire una univoca e universale comprensione, che è poi il razionale alla base del SI.

----------

[1] Istat. Principali dimensioni geostatistiche e grado di urbanizzazione del Paese. Superficie territoriale per zona altimetrica.

https://www.istat.it/non-categorizzato/principali-dimensioni-geostatistiche-e-grado-di-urbanizzazione-del-paese/

[2] DECRETO DEL PRESIDENTE DELLA REPUBBLICA 12 agosto 1982, n. 802 Attuazione della direttiva (CEE) n. 80/181 relativa alle unita' di misura. GU Serie Generale n.302 del 03-11-1982 - Suppl. Ordinario.

https://www.gazzettaufficiale.it/eli/id/1982/11/03/082U0802/sg

[3] Per una introduzione al SI, che riporta anche le indicazioni delle modifiche apportate al sistema dopo l'adesione ufficiale dell'Italia avvenuta nel 1982, vedere: Grandezze e unità di misura. Breve storia dall'antichità al Sistema Internazionale di Unità (SI).

[4] Sul sito del Bureau International des Poids et Mesures - in una delle due sole lingue adottate, inglese e francese - si trova il documento ufficiale "SI Brochure: The International System of Units (SI)" ovvero "Brochure sur le SI: Le Système international d'unités".

https://www.bipm.org/en/publications/si-brochure

[5] La CGPM (Conférence Générale des Poids et Mesures) viene convocata periodicamente, ogni quattro o sei anni, e discute e approva unità, terminologia e raccomandazioni del Sistema internazionale di unità (SI). 

[6] Unicode Explorer, U+00A0 NO-BREAK SPACE

https://unicode-explorer.com/c/00A0

[7] Come illustrato nel post Importazione dei dati da un file .csv e nel post Esportazione dei dati in un file .csv.

[8] Vedere: Grandezze e unità di misura. Breve storia dall'antichità al Sistema Internazionale di Unità (SI), p. 47.

[9] Vedere il post Esprimere i numeri in formato fisso.