Grafici di dispersione (scatterplot) con ggplot

I grafici di dispersione (scatter plot o scatterplot) forniscono un ottimo esempio delle potenzialità delle funzioni del pacchetto ggplot2 [1] nella rappresentazione grafica dei dati. Funzioni che possono risultare ostiche a chi le affronta per la prima volta, ma che consentono risultati che non si riescono a ottenere impiegando esclusivamente le funzioni base di R [2].

Oltre al pacchetto ggplot2 bisogna avere installato – o bisogna scaricare anche – il pacchetto DAAG [3] che contiene i dati impiegati nell'esempio e il pacchetto gridExtra che nel nostro caso è necessario per combinare più grafici in una sola figura. 

Copiate e incollate nella Console di R questo script e premete ↵ Invio.

# SCATTERPLOT con ggplot 

# 

library(DAAG) # carica il pacchetto DAAG che include il set di dati ais

library(ggplot2) # carica il pacchetto per la grafica

library(gridExtra) # carica il pacchetto per combinare i grafici in una sola figura

#

# scatterplot 

plot1 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point()

#

# con regressione loess

plot2 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point() + geom_smooth()

#

# con regressione lineare

plot3 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point() + geom_smooth(method="lm")

#

# con la densità di distribuzione

plot4 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color="red")) + geom_density_2d() + theme_classic() + labs(title="Densità di distribuzione \n tutti i casi", x="Eritrociti in 10^6/μL", y="Emoglobina in g/dL") + theme(plot.title=element_text(hjust=0.5), legend.position="none")

#

# combina i grafici in una sola figura

grid.arrange(plot1, plot2, plot3, plot4, nrow=2, ncol=2) 

#

Lo script è semplice: dopo avere caricato i pacchetti necessari, sono generati quattro grafici che sono salvati separatamente per essere poi, al termine, combinati in una sola figura.

Per realizzare il primo grafico (plot1) viene impiegata la funzione ggplot() che inizializza l'oggetto al quale sono collegate con il segno più [+] le successive funzioni, che sviluppano la grafica e che prevede:

→ come primo argomento il nome della tabella che contiene i dati (ais) [3];

→ come secondo argomento la funzione aes() che specifica la variabile da riportare in ascisse (rcc) e la variabile da riportare in ordinate (hg), che sono rispettivamente la concentrazione degli eritrociti nel sangue espressa in milioni per microlitro di sangue (10^6/µL) e la concentrazione di emoglobina espressa in grammi per decilitro di sangue (g/dL).

Alla funzione ggplot() viene quindi collegata con il segno più [+] la funzione geom_point() che realizza il grafico xy lasciando per tutti gli argomenti i valori previsti di default.

Da notare subito che questa è la struttura base che rimane identica in tutti e quattro i grafici realizzati, che si differenziano tra loro per le componenti grafiche via via aggiunte.

Il secondo grafico (plot2) quindi riprende tal quale la precedente struttura base e aggiunge semplicemente tramite la funzione geom_smooth(), la regressione loess prevista di default, con i suoi limiti di confidenza (la regressione loess è una regressione che collega tra loro una serie di regressioni polinomiali, quelle che localmente meglio si adattano ai dati).

Nel terzo grafico (plot3) impiegando l'argomento method la regressione loess è sostituita con la usuale retta di regressione ("lm"), riportando anche in questo caso i limiti i confidenza. Se non li volete rappresentare correggete la riga di codice sostituendola completamente con la seguente o semplicemente aggiungendo quanto qui riportato in colore 

# con regressione lineare

plot3 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point() + geom_smooth(method="lm", se=FALSE)

#

Il quarto grafico (plot4) riprende la struttura base aggiungendo:

→ con aes(color="red") un colore ai punti che rappresentano i dati;

→ con la funzione geom_density_2d() la rappresentazione sul piano dei livelli di densità nella distribuzione dei dati;

→ con la funzione theme_classic() il cambiamento di stile che risulta evidente nell'ultimo grafico;

→ con la funzione labs() il titolo e le etichette degli assi, Da notare il simbolo \n che all'interno di una stringa di testo determina il ritorno a capo;

→ con la funzione theme() il codice (abbastanza arzigogolato) che determina la centratura del titolo e il valore "none" per l'argomento legend.position che determina la posizione della legenda, che pertanto non viene riportata.

Infine con la funzione grid.arrange() i quattro grafici sono combinati in un'unica figura.

Ora copiate e incollate nella Console di R questo secondo script che ha come obiettivo evidenziare la semplicità con la quale possiamo effettuare in un grafico rappresentazioni separate in base a un fattore che nel nostro caso è la variabile sesso (sex), in quanto il set di dati ais contiene dati ematologici e dati biometrici, rilevati in atleti australiani sia di sesso femminile sia di sesso maschile.

# SCATTERPLOT con ggplot 

# colori differenziati in base a un fattore

# 

library(DAAG) # carica il pacchetto DAAG che include il set di dati ais

library(ggplot2) # carica il pacchetto per la grafica

library(gridExtra) # carica il pacchetto per combinare i grafici in una sola figura

#

# scatterplot per sesso

plot1 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex))

#

# con simboli dei punti differenziati

plot2 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none")

#

# con rette di regressione e limiti di confidenza

plot3 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none") + geom_smooth(aes(group=sex, color=sex), method="lm", se=TRUE)

#

# con rette di regressione estese

plot4 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none") + geom_smooth(aes(group=sex, color=sex), method="lm", se=FALSE, fullrange=TRUE)

#

# combina i grafici in una sola figura

grid.arrange(plot1, plot2, plot3, plot4, nrow=2, ncol=2) 

#

Per realizzare il primo grafico (plot1) viene impiegata la struttura base già vista nello script precedente, ma con la semplice aggiunta a geom.point della funzione aes() che con l'argomento color posto uguale a sex riporta i dati con un colore differenziato in base al sesso.

Il secondo grafico (plot2) riprende tal quale il codice precedente ma:

→ alla funzione geom_point() aggiunge l'argomento shape=sex che automaticamente riporta un simbolo differente in base al sesso;

→ con la funzione theme() esclude dal grafico la legenda.

Il terzo grafico (plot3) è identico al secondo ma con la funzione geom_smooth() aggiunge la retta di regressione ordinaria (method="lm") con i limiti di confidenza (se=TRUE) separatamente (group=sex) e con un colore diverso (color=sex) per ciascun sesso.

Il quarto grafico (plot4) riprende esattamente il codice del terzo ma con se=FALSE esclude la rappresentazione dei limiti di confidenza e con fullrange=TRUE riporta la retta di regressione a tutto campo e al di la dei limiti dei dati osservati (per inciso si ricorda che, a meno di casi particolari e adeguatamente giustificati, l'estrapolazione non andrebbe mai fatta, ma viene qui riportata per completezza).

Infine con la funzione grid.arrange() i quattro grafici sono di nuovo combinati, per semplicità, in un'unica figura.

Ora copiate e incollate nella Console di R questo script e premete ↵ Invio.

# SCATTERPLOT con ggplot 

# dati con densità delle distribuzioni

# 

library(DAAG) # carica il pacchetto DAAG che include il set di dati ais

library(ggplot2) # carica il pacchetto per la grafica

library(gridExtra) # carica il pacchetto per combinare i grafici in una sola figura

#

# scatterplot con ellissi

plot1 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none") + stat_ellipse(aes(color=sex))

#

# con densità di distribuzione della y

plot2 <- ggplot(ais, aes(y=hg, fill=sex)) + geom_density(alpha=0.5) + theme(legend.position="none")

#

# con densità di distribuzione della x

plot3 <- ggplot(ais, aes(x=rcc, fill=sex)) + geom_density(alpha=0.5) + theme(legend.position="none")

#

# con livelli di densità separati per sesso

plot4 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none") + geom_density_2d(aes(color=sex))

#

# combina i grafici in una sola figura

grid.arrange(plot1, plot2, plot3, plot4, nrow=2, ncol=2) 

#

Il primo grafico (plot1) riprende le funzioni già note, ma aggiunge, con la funzione stat_ellipse(), le ellissi che riportano i limiti di confidenza al 95% delle distribuzioni dei dati, separate per ciascun sesso e ulteriormente analizzate con il secondo e il terzo grafico.

Il secondo grafico (plot2) riporta in ordinate per la variabile emoglobina (y=hg) e separatamente per ciascun sesso (fill=sex), con la funzione geom_density(), il kernel density plot, con un colore trasparente al 50% (alpha=0.5) per consentirne la sovrapposizione. Da notare due aspetti non banali gestiti automaticamente dalle funzioni qui impiegate: gli assi sono ruotati nella posizione corretta e per l'asse delle ordinate la scala nella quale sono espressi i valori di concentrazione dell'emoglobina (hg) è allineata con quella del primo grafico.

Il terzo grafico (plot3) riporta in modo analogo ma in ascisse il kernel density plot per sesso della variabile concentrazione degli eritrociti (x=rcc). Da notare che anche in questo caso gli assi sono automaticamente ruotati nella posizione corretta e per l'asse delle ascisse la scala nella quale sono espressi i valori di concentrazione degli eritrociti (rcc) è automaticamente allineata con quella del primo grafico.

In definitiva i primi tre grafici formano un tutt'uno organico – con le variabili rappresentate contemporaneamente sia singolarmente in forma di grafico xy sia in forma di grafici che ne riportano in continuo la densità (kernel density plot) – che fornisce un'analisi molto interessante dei dati, mostrando come la distribuzione dei valori di concentrazione dell'emoglobina nel sangue differisce nei due sessi.

Il quarto grafico (plot4) riprende esattamente il primo aggiungendo questa volta al posto delle ellissi con la funzione geom_density_2d() la rappresentazione sul piano dei livelli di densità nella distribuzione dei dati.

Se vedendo il grafico notate che preferireste (io lo preferisco di gran lunga) che i due kernel density plot fossero riferiti al grafico in basso a destra, niente di più facile, copiate e incollate nella Console di R questo script e premete ↵ Invio.

# SCATTERPLOT con ggplot 

# dati con densità delle distribuzioni

# 

library(DAAG) # carica il pacchetto DAAG che include il set di dati ais

library(ggplot2) # carica il pacchetto per la grafica

library(gridExtra) # carica il pacchetto per combinare i grafici in una sola figura

#

# scatterplot con ellissi

plot1 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none") + stat_ellipse(aes(color=sex))

#

# con densità di distribuzione della y

plot2 <- ggplot(ais, aes(y=hg, fill=sex)) + geom_density(alpha=0.5) + theme(legend.position="none") + scale_x_reverse()

#

# con densità di distribuzione della x

plot3 <- ggplot(ais, aes(x=rcc, fill=sex)) + geom_density(alpha=0.5) + theme(legend.position="none")

#

# con livelli di densità separati per sesso

plot4 <- ggplot(ais, aes(x=rcc, y=hg)) + geom_point(aes(color=sex, shape=sex)) + theme(legend.position="none") + geom_density_2d(aes(color=sex))

#

# combina i grafici in una sola figura

grid.arrange(plot1, plot3, plot2, plot4, nrow=2, ncol=2) 

#

Come si vede il codice è identico al precedente, a parte il fatto che dovete:

→ scambiare tra di loro i grafici (plot3, plot2,) quando li combinate in un'unica figura (ultima riga di codice), portando quindi il kernel density plot degli eritrociti (rcc) in alto a destra e quello dell'emoglobina (hg) in basso a sinistra; 

→ aggiungere con (+) al plot2 la funzione scale_x_reverse() per invertire la scala dell'asse delle ascisse e quindi la rappresentazione del kernel density plot.

Ricordate, perché prima o poi vi tornerà utile, che qualora fosse necessario potete anche invertire la scala dell'asse delle ordinale con scale_y_reverse() e scambiare di posizione gli assi con coord_flip(). 

Concludiamo con questo script, copiatelo e incollatelo nella Console di R e premete ↵ Invio:

# GRAFICO DI DISPERSIONE con ggplot

# colori differenziati in base a un fattore

#

library(DAAG) # carica il pacchetto che include il set di dati ais

library(ggplot2) # carica il pacchetto per la grafica

#

windows() # apre e inizializza una nuova finestra grafica

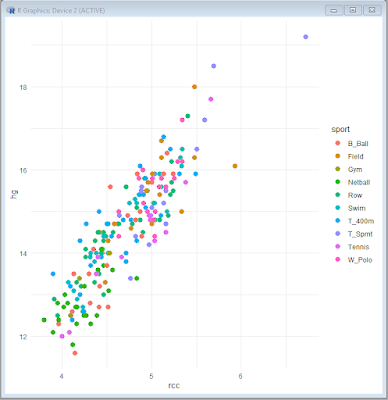
ggplot(ais, aes(x=rcc, y=hg, color=sport)) + geom_point(size=3) + theme_minimal() # traccia il grafico

#

Ed ecco il grafico

che ci consente di mostrare come la funzione ggplot() sia in grado di coniugare semplicità e potenza nella rappresentazione dei grafici di dispersione (scatterplot).

Sono infatti sufficienti come argomenti della funzione solamente:

→ la tabella che include i dati (ais);

→ la x (rcc) e la y (hg) da rappresentare;

→ l'indicazione della variabile "fattore" (sport) che contiene i valori (lo sport praticato) sulla base dei quali attribuire ai punti un differente colore (color=);

mentre sono facoltativi e aggiunti solamente per completezza la dimensione dei punti (size=3) e la funzione theme_minimal() che toglie il colore grigio di sfondo.

Conclusione: questa breve presentazione ha voluto evidenziare come le funzioni incluse nel pacchetto ggplot2 possono sia essere impiegate in modo agevole, sia fornire un importante aiuto nella introspezione dei dati e nella comunicazione dell'informazione in essi contenuta [4]. 

----------

[1] Vedere la documentazione e il manuale di riferimento su:

https://cran.r-project.org/web/packages/ggplot2/index.html

[2] Vedere il post Grafici di dispersione (scatterplot).

[3] Vedere il post Il set di dati ais nel quale trovate anche come caricare i dati senza impiegare il pacchetto DAAG. 

[4] Ovviamente potete procedere con ulteriori approfondimenti impiegando la documentazione del pacchetto [1], ma potete anche valutare al bisogno l'opportunità di ricorrere a qualcuno dei corsi sull'argomento disponibili sul web, cito per tutti un esempio, "Introduction to Data Visualization with ggplot2":

https://www.datacamp.com/courses/introduction-to-data-visualization-with-ggplot2

Regressione polinomiale di terzo grado

Supponiamo di avere, per ciascuno di una serie di valori prefissati x (riportati in ascisse), il risultato di altrettante misure y (riportate in ordinate) e con la funzione plot() visualizziamo i dati sotto forma di un grafico xy.

Copiate il codice che segue nella Console di R e premete ↵ Invio:

#

x <- c(20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300) # valori in ascisse

y <- c(0.695, 0.699, 0.707, 0.722, 0.740, 0.765, 0.790, 0.815, 0.840, 0.865, 0.885, 0.902, 0.920, 0.932, 0.940) # valori in ordinate

plot(y~x, col="black", pch=1, main="Grafico xy", xlab="Valori prefissati (x)", ylab="Risultati delle misure effettuate (y)") # traccia il grafico xy

#

Dalla ispezione del grafico risulta evidente una relazione non lineare.

Questo ci fa escludere la possibilità di descrivere la relazione di funzione che intercorre tra le due variabili mediante una retta. E pone il tema di quale sia la curva che potrebbe meglio descriverla.

La prima cosa da valutare è se esiste un modello deterministico di un evento fisico, chimico-fisico, biologico, econometrico o quant'altro, che si assume descriva adeguatamente la relazione di funzione che intercorre tra le due variabili: in tal caso non resta che applicare l'equazione fornita dal modello. In caso contrario è necessario ricorrere ad un modello empirico: ed è questo che consideriamo essere il caso nostro.

Qualora si debba ricorrere ad un modello empirico, la regola fondamentale è impiegare l'equazione più semplice compatibile con una adeguata descrizione dei dati. Nel nostro caso visto che è evidente dall'ispezione del grafico che l'equazione di una retta 

y = a + b· ​⁠⁠x

calcolata mediante la classica regressione lineare con il metodo dei minimi quadrati sarebbe inadeguata a descrivere la relazione di funzione che lega la y alla x, possiamo pensare di ricorrere ad una equazione appena più complessa, come quella fornita da una regressione polinomiale di secondo grado nella forma

y = a + b· x + c· x²

e calcolata anch'essa con il metodo dei minimi quadrati [1].

Copiate lo script nella Console di R e premete ↵ Invio: 

# REGRESSIONE POLINOMIALE di secondo grado

#

x <- c(20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300) # valori in ascisse

y <- c(0.695, 0.699, 0.707, 0.722, 0.740, 0.765, 0.790, 0.815, 0.840, 0.865, 0.885, 0.902, 0.920, 0.932, 0.940) # valori in ordinate

#

options(scipen=999) # esprime i numeri in formato fisso

#

# calcola la regressione 

#

polisec <- lm(y~poly(x, degree=2, raw=TRUE)) # calcola la regressione

summary(polisec) # riporta le statistiche della regressione

#

# traccia il grafico

#

newx <- seq(min(x), max(x), (max(x)-min(x))/1000) # valori x in corrispondenza dei quali calcolare il valore del polinomio

newy <- predict(polisec, list(x=newx)) # calcola il valore corrispondente del polinomio

plot(y~x, col="black", pch=1, main="Regressione polinomiale di secondo grado", xlab="Valori prefissati (x)", ylab="Risultati delle misure effettuate (y)") # predispone il grafico e riporta i dati

lines(newx, newy, col="black", lty=2, lwd=1) # traccia il polinomio

#

options(scipen=0) # ripristina la notazione scientifica

#

La prima cosa che notiamo è che il polinomio di secondo grado descrive in pratica una retta.

Inoltre se andate alla quinta riga di codice tra le statistiche generate con la funzione summary(polisec) trovate:

Coefficients:

                                     Estimate   Std. Error t value             Pr(>|t|)    

(Intercept)                      0.6573076923 0.0100102431  65.664 < 0.0000000000000002 ***

poly(x, degree = 2, raw = TRUE)1 0.0009554000 0.0001439488   6.637             0.000024 ***

poly(x, degree = 2, raw = TRUE)2 0.0000001299 0.0000004374   0.297                0.772    

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Mentre l'intercetta a con un p=0.0000000000000002 e il coefficiente di primo grado b del polinomio con un p=0.000024 sono significativi, il coefficiente di secondo grado c con un p=0.772 non lo è affatto. Pertanto l'equazione del polinomio di secondo grado

y = a + b· x + c· x²  

privata del coefficiente c· x² si riduce all'equazione di una retta

y = a + b · x   

cosa che conferma il grafico ottenuto.

Dati che descrivono una curva con un raggio di curvatura omogeneo, senza massimi, senza minimi e senza punti di flesso - cioè senza punti di passaggio tra due curvature che vanno in senso opposto - sono compatibili con il ramo di una parabola descritta appunto da un polinomio di secondo grado. Ma in questo caso i dati presentano un punto di flesso tra una curvatura iniziale rivolta verso l'alto e una curvatura finale rivolta verso il basso. Il polinomio di secondo grado media tra le due, finendo con il fornire una curvatura talmente ridotta da potere essere assimilata ad una retta.

Dobbiamo pertanto vedere cosa accade applicando il modello immediatamente successivo, rappresentato da una regressione polinomiale di terzo grado nella forma

 y = a + b· x + c· x² + d· x³     

Copiate lo script nella Console di R e premete ↵ Invio: 

# REGRESSIONE POLINOMIALE di terzo grado

#

x <- c(20, 40, 60, 80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300) # valori in ascisse

y <- c(0.695, 0.699, 0.707, 0.722, 0.740, 0.765, 0.790, 0.815, 0.840, 0.865, 0.885, 0.902, 0.920, 0.932, 0.940) # valori in ordinate

#

options(scipen=999) # esprime i numeri in formato fisso

#

# calcola la regressione 

#

politer <- lm(y~poly(x, degree=3, raw=TRUE)) # calcola la regressione

summary(politer) # riporta le statistiche della regressione

#

# traccia il grafico

#

newx <- seq(min(x), max(x), (max(x)-min(x))/1000) # valori x in corrispondenza dei quali calcolare il valore del polinomio

newy <- predict(politer, list(x=newx)) # calcola il valore corrispondente del polinomio

plot(y~x, col="black", pch=1, main="Regressione polinomiale di terzo grado", xlab="Valori prefissati (x)", ylab="Risultati delle misure effettuate (y)") # predispone il grafico e riporta i dati

lines(newx, newy, col="black", lty=2,lwd=1) # traccia il polinomio

#

options(scipen=0) # ripristina la notazione scientifica

#

Le prime due righe di codice servono semplicemente ad assegnare (<-) i valori inclusi nella funzione c() al vettore x e al vettore y che in questo modo conterranno i nostri dati.

Poi mediante la funzione options() con l'argomento scipen=999 facciamo si che i risultati siano espressi in formato fisso, cosa che li renderà meglio leggibili (questo almeno a mio modo di vedere: se volete lasciare i risultati nella notazione scientifica eliminate questa riga di codice o, forse meglio, anteponete a questa riga di codice il simbolo #).

La quarta riga di codice assegna (<-) all'oggetto politer i risultati del calcolo della regressione polinomiale y~poly(x) di terzo grado (degree=3), l'argomento raw=TRUE è impiegato perché non ci interessano i polinomi ortogonali (l'opzione di default è raw=FALSE).

Se siete interessati ad approfondimenti, ricordo che potete visualizzare ad esempio la struttura dell'oggetto politer digitando str(politer) e potete avere informazioni sulle funzioni impiegate nello script digitando help(nomedellafunzione).

Alla quinta riga di codice la funzione summary(politer) consente infine di visualizzare le statistiche generate:

Call:

lm(formula = y ~ poly(x, degree = 3, raw = TRUE))

Residuals:

       Min         1Q     Median         3Q        Max 

-0.0032624 -0.0012957  0.0006167  0.0014060  0.0019740 

Coefficients:

                                         Estimate       Std. Error t value             Pr(>|t|)    

(Intercept)                       0.6966205128205  0.0025292032241 275.431 < 0.0000000000000002 ***

poly(x, degree = 3, raw = TRUE)1 -0.0003180913177  0.0000662417487  -4.802             0.000552 ***

poly(x, degree = 3, raw = TRUE)2  0.0000097653837  0.0000004730826  20.642       0.000000000381 ***

poly(x, degree = 3, raw = TRUE)3 -0.0000000200739  0.0000000009739 -20.612       0.000000000387 ***

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.001865 on 11 degrees of freedom

Multiple R-squared:  0.9997,    Adjusted R-squared:  0.9996 

F-statistic: 1.081e+04 on 3 and 11 DF,  p-value: < 0.00000000000000022

La voce Residuals riporta le statistiche delle differenze che, dopo l'approssimazione dei punti con il polinomio di terzo grado, residuano tra i punti stessi e la curva calcolata: differenze piccole come quelle qui osservate indicano un'ottima approssimazione della curva ai dati.

La voce Coefficients riporta dall'alto verso il basso il valore stimato (Estimate) dell'intercetta a (0.6966205128205), del coefficiente di primo grado b (-0.0003180913177), del coefficiente di secondo grado c (0.0000097653837) e del coefficiente di terzo grado d (-0.0000000200739) e ci consente di scrivere l'equazione del polinomio che sarà quindi 

y = 0.6966205128205 - 0.0003180913177· x + 0.0000097653837· x² - 0.0000000200739· x³     

   

Per ciascun coefficiente viene calcolato il valore del test t di Student come rapporto tra il valore stimato (Estimate) e il suo errore standard (Std. Error) e viene infine riportato il valore di probabilità (Pr(>|t|)) di osservare per caso il valore di t riportato: se tale probabilità è sufficientemente bassa ci assumiamo il rischio di considerare significativo il coefficiente in questione. Nel nostro caso essendo i valori di p sempre molto piccoli (di gran lunga inferiori al valore p = 0.05 generalmente considerato come valore soglia per la significatività) possiamo affermare che tutti e tre i coefficienti del polinomio di terzo grado sono significativi e lo rendono un'equazione in grado di descrivere adeguatamente i dati forniti. 

Il coefficiente di correlazione multipla R² (Multiple R-squared: 0.9997) molto elevato  con una statistica F significativa (p-value: < 0.00000000000000022) conferma ulteriormente la bontà dell'approssimazione. E niente meglio del grafico dei punti e del polinomio che li approssima può confermarla.

Il grafico è tracciato in modo da garantire una risoluzione grafica elevata:

→ l'intervallo compreso tra il valore minimo min(x) e il valore massimo max(x) della variabile in ascisse viene suddiviso per ottenere 1000 valori (ma potete cambiarne il numero) salvati nell'oggetto newx e in corrispondenza dei quali calcolare il valore del polinomio;

→ con la funzione predict() sono calcolati e riportati nell'oggetto newy i valori delle ordinate del polinomio corrispondenti ai valori delle ascisse contenuti in newx ;

→ la funzione plot() viene impiegata per riportare sul grafico di dati contenuti in x e in y;

→ la funzione lines() viene impiegata per sovrapporre ai dati il polinomio.

Potete riportare i dati modificando il simbolo impiegato (pch=...) e il suo colore (col="..."), come pure tracciare il polinomio modificando l'aspetto o stile della linea tracciata (lty=...), il suo colore (col="...") e il suo spessore (lwd=...) [2].

Da notare che il grafico è stato tracciato esclusivamente all'interno dei dati, quindi in un'ottica di interpolazione: e questo ci ricorda anche che, trattandosi di un modello empirico, è da escludere l'impiego del polinomio per la estrapolazione, cioè per trarre conclusioni al di fuori dei dati impiegati per calcolarlo. 

A chiudere lo script è la funzione options() che con l'argomento scipen=0 ripristina l'espressione dei numeri nella notazione scientifica [3].

Lo script può essere riutilizzato semplicemente riportando manualmente in x e in y i nuovi dati, o meglio ancora importandoli da un file [4].

----------

[1] Il metodo dei minimi quadrati prevede - ed è quello che abbiamo assunto essere il nostro caso - che la variabile in ascisse (x) abbia valori prefissati, che la variabile in ordinate (y) sia rappresentata da misure (affette da un errore casuale distribuito normalmente) effettuate corrispondenza delle x e minimizza la somma dei quadrati delle differenze y - y' ovvero delle differenze tra ciascun valore misurato y e il valore y' = f(x) corrispondente calcolato mediante la regressione (lineare o polinomiale). Esempi possono essere la risposta y di un sensore misurata in corrispondenza di una serie di concentrazioni date x di una sostanza chimica, la misurazione di un evento y in corrispondenza di una serie data di tempi x, e così via.

[2] Trovate le relative indicazioni:

→ nel post Cambiare i simboli dei punti di R, 

→ nel post Visualizzare i colori disponibili in R 

→ nel post Cambiare gli stili delle linee di R

[3] La notazione scientifica è una notazione esponenziale, cioè una notazione che consente di scrivere un numero N assegnato come prodotto di un opportuno numero a per la potenza di un altro numero b^k essendo b la base della notazione esponenziale. In particolare la notazione scientifica è una notazione esponenziale in base 10 (b = 10). Tuttavia "notazione esponenziale" non è sinonimo di "notazione scientifica" in quanto esistono notazioni esponenziali che impiegano una base diversa da quella impiegata dalla notazione scientifica: ne sono un esempio la notazione esponenziale in base 2 (b = 2) impiegata in informatica, e la notazione esponenziale in base e (b = e) - essendo il numero di Nepero e = 2.718 281 828 459... - impiegata in campo matematico e in campo scientifico.

[Precisazione aggiuntiva: in R il separatore delle cifre decimali è il punto (.) e come già riportato altrove questa convenzione per ragioni di omogeneità viene adottata non solo negli script ma anche nei file di dati e in tutto il testo di questo sito, quindi anche nell'espressione del numero e di Nepero. Per le norme che regolano la punteggiatura all'interno dei numeri rimando al post Come separare i decimali e come raggruppare le cifre].

[4]  Alla pagina Indice nel capitolo R - gestione dei dati trovate i collegamenti ai post che contengono gli script per importare i dati da file esterni.