Analisi della varianza a un fattore

Anche se può sembrare paradossale, l'analisi della varianza consente di effettuare il confronto tra medie. Infatti come è stato sottolineato, a dispetto della “... apparente incoerenza della nomenclatura – il fatto cioè che le tecniche riguardino confronti di medie piuttosto che varianze – ... il complesso delle tecniche chiamato analisi della varianza costituisce un potente metodo per analizzare il modo in cui il valore medio di una variabile è influenzato da classificazioni di vario genere dei dati” [1].

Ancor più direttamente Wonnacott all'inizio del capitolo dedicato all'analisi della varianza riporta: "... abbiamo compiuto inferenze relative alla media di una popolazione ... abbiamo esteso il ragionamento alla differenza fra due medie ... vogliamo confrontare ora r medie, usando un insieme di tecniche che vengono comunemente denominate «analisi della varianza»" [2].  

Le tecniche di analisi della varianza (ANOVA) sono ampiamente trattate in tutti i testi di statistica, ai quali si rimanda per i necessari approfondimenti. Vediamo in questo post la più semplice di queste tecniche, l'analisi della varianza a un fattore che:

→ è "... una generalizzazione del test t [di Student] per [il confronto tra medie di] dati non appaiati [due campioni indipendenti], adatta a un numero qualunque di gruppi ..." [1];

→ è "... equivalente al test t per [il confronto tra medie nel caso di] dati non appaiati quando i gruppi sono ... due" [1];

→ è basata "... su due importanti ipotesi: (a) la normalità delle distribuzioni delle osservazioni ... e (b) la costanza delle varianze nei diversi gruppi" [3].

Per la verifica preliminare della omogeneità delle varianze (b) si rimanda al post che tratta il test di Levene nel quale sono riportati anche i riferimenti ai test che possono essere eseguiti per verificare (a) ovvero la normalità delle distribuzioni dei dati [4].

I problemi che si presentano nella pratica quando gli assunti alla base del modello statistico dell'ANOVA non sono completamente soddisfatti – e i correttivi che possono eventualmente essere adottati – vanno al di la dei limiti di questo blog, ma sono ben approfonditi per esempio da Snedecor [5].

Per lo script impieghiamo i dati riportati da Wonnacott che riguardano "... tre macchine (A, B e C), le quali, essendo azionate da uomini e a causa di altre ragioni inesplicabili, danno luogo ad un prodotto orario soggetto a fluttuazioni casuali. Nella speranza di «mediare» e quindi di ridurre gli effetti di tali fluttuazioni, si effettua un campione casuale di 5 ore per ciascuna macchina, i cui risultati sono raccolti nella Tabella 10-1 insieme con le relative medie" [6].

La domanda è: le differenze tra le medie di produzione 48.6, 56.4 e 51.6, riportate nell'ultima colonna sulla destra, possono essere attribuite al caso? Se così non fosse, dovremmo pensare che esiste qualcosa in grado di influenzare la produzione media delle macchine.

I dati riportati in forma di tabella da Wonnacott per essere analizzati con R devono essere organizzati in un file di testo, sotto forma di righe (record) contenenti ciascuna due variabili (campi), una variabile qualitativa (fattore) che indica la macchina, e una variabile numerica che indica la produzione della macchina, e assumono quindi la forma seguente:

macchina;produzione
i1;48.4
i1;49.7
i1;48.7
i1;48.5
i1;47.7
i2;56.1
i2;56.3
i2;56.9
i2;57.6
i2;55.1
i3;52.1
i3;51.1
i3;51.6
i3;52.1
i3;51.1

Copiate le sedici righe riportate qui sopra aggiungendo un ↵ Invio al termine dell'ultima riga e salvatele in C:\Rdati\ in un file di testo denominato anova1.csv (attenzione all'estensione .csv al momento del salvataggio del file).

In alternativa andate alla pagina Dati nella quale trovate diverse opzioni per scaricare i file di dati, quindi copiate il file anova1.csv nella cartella C:\Rdati\

Poi scaricate dal CRAN e installate il pacchetto ggplot2, con il quale realizzeremo una rappresentazione grafica dei dati integrativa all'analisi statistica.

Infine copiate e incollate nella Console di R questo script e premete ↵ Invio:

 

# ANOVA analisi della varianza a un fattore
#

mydata <- read.table("c:/Rdati/anova1.csv", header=TRUE, sep=";", dec=".") # importa i dati

#

anova1 <- aov(produzione~macchina, data=mydata) # esegue l'analisi della varianza
summary(anova1) # mostra i risultati dell'analisi della varianza
#
pairwise.t.test(mydata$produzione, mydata$macchina, p.adjust.method = "bonferroni") # confronto tra le (produzioni) medie delle macchine impiegando il test t con la correzione di Bonferroni per confronti multipli
#

Lo script è suddiviso in tre blocchi di codice. Nel primo sono importati i dati con la funzione read.table().

Nel secondo viene eseguita l'analisi della varianza a un fattore mediante la funzione aov() (seconda riga) e sono riepilogati (terza riga) i risultati con la funzione summary():

> summary(anova1) # mostra i risultati dell'analisi della varianza

            Df Sum Sq Mean Sq F value   Pr(>F)    

macchina     2 154.80   77.40   141.6 4.51e-09 ***
Residuals   12   6.56    0.55                     
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

La varianza (Mean Sq) è calcolata dividendo la somma degli scarti quadratici (Sum Sq) per i gradi di libertà (Df). Il valore F (141.6) del rapporto fra varianze (F value) viene calcolato dividendo la varianza dovuta alle macchine (77.40) per la varianza residua (0.55).

La probabilità (Pr(>F)) è la probabilità di osservare per caso il valore F (141.6) e consente di rispondere alla domanda: le differenze tra le medie di produzione possono essere attribuite al caso? Essendo tale probabilità 4.51e-09 o se preferite 0.0000000451, quindi molto inferiore al valore 0.05 assunto in genere come valore soglia, concludiamo che le differenze tra le medie di produzione non sono attribuibili al caso: le medie sono significativamente diverse, quindi esiste qualcosa in grado di influenzare la produzione [media] delle macchine. 

Da notare una cosa molto importante: l'ANOVA è un test globale e ci dice che tra le medie [nel nostro caso tra le medie di produzione delle tre macchine] esiste una differenza significativa, ma non consente di individuare la/e media/e causa della significatività. In altre parole non ci dice se la significatività sia dovuta alla differenza tra la prima macchina e la seconda, tra la prima macchina e la terza, tra la seconda macchina e la terza, o a una qualche combinazione di queste tre possibilità. Se è questo che interessa, è possibile ricorrere a test alternativi (vedi sotto).

Il terzo blocco di codice consiste anch'esso in una sola riga. Abbiamo già visto che l'analisi della varianza a un fattore è una generalizzazione del test t di Student per dati non appaiati, ed è equivalente al test t quando i gruppi sono due [7]. Tuttavia esistono delle correzioni del test t che consentono di impiegarlo anche nel caso del confronto di più di due gruppi [8], ed è proprio una di queste, la correzione di Bonferroni (p.adjust.method = "bonferroni"), che viene qui applicata ai dati mediante la funzione pairwise.t.test() per confrontarne i risultati con quelli dell'ANOVA

pairwise.t.test(mydata$produzione, mydata$macchina, p.adjust.method = "bonferroni") # confronto tra le (produzioni) medie delle macchine impiegando la correzione di Bonferroni per confronti multipli

        Pairwise comparisons using t tests with pooled SD 

data:  mydata$produzione and mydata$macchina 

   i1      i2     

i2 3.4e-09 -      

i3 1.0e-04 8.1e-07

P value adjustment method: bonferroni 

Come si vede il test t effettuato per tutti e tre i confronti possibili tra macchine conferma i risultati dell'ANOVA riportando differenze sempre significative – essendo sempre inferiori a 0.05 le probabilità che le differenze tra medie qui osservate siano dovute al caso – ma ci indica anche dove risiedono tali differenze, riportando separatamente che i1 <> i2 (p=3.4e-09), i1 <> i3 (p=1.0e-04), i2 <> i3 (p=8.1e-07), cosa che l'ANOVA, essendo un test globale, non consente di specificare (vedi sopra). 

Altre correzioni alternative, meno conservative della correzione di Bonferroni [9], possono essere impiegate con l'argomento p.adjust.method = : secondo Holm (1979) ("holm"), Hochberg (1988) ("hochberg"), Hommel (1988) ("hommel"), Benjamini & Hochberg (1995) ("BH" o "fdr"), Benjamini & Yekutieli (2001) ("BY"), e "none" per nessuna correzione.

Se installate  la libreria ggplot2 potete realizzare un grafico a punti (dotplot) [10] che consente di visualizzare i dati: il che è sempre un importante complemento all'analisi numerica. Copiate e incollate nella Console di R questo script e premete ↵ Invio:

 

#

library(ggplot2) # carica il pacchetto per la grafica

#

ggplot(mydata, aes(x=macchina, y=produzione, fill=macchina)) + geom_dotplot(binaxis='y', stackdir='center', stackratio=1, dotsize=1, binwidth=0.4, show.legend=FALSE) + coord_cartesian(ylim=c(40, 60)) + labs(title="Variabilità osservata nella produzione tra le macchine", x="Macchina impiegata", y="Produzione realizzata") + theme_classic() # dotplot della produzione per macchina

#

Se l'ANOVA consente di effettuare un confronto tra medie, a questo punto sembra logico sovrapporre ai dati raccolti la loro media e la loro deviazione standard.

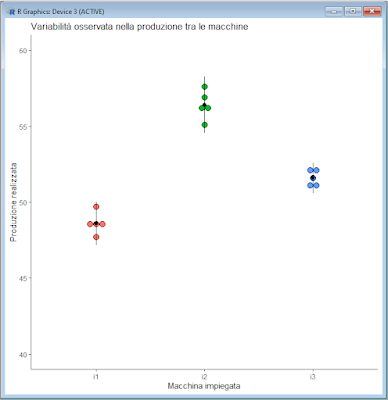
Copiate e incollate nella Console di R queste due righe di codice che aprono una nuova finestra grafica nella quale viene rappresentato il grafico precedente sovrapponendo poi ai punti la media con l'intervallo corrispondente a due deviazioni standard:

#

windows() # apre e inizializza una nuova finestra grafica

#
ggplot(mydata, aes(x=macchina, y=produzione, fill=macchina)) + geom_dotplot(binaxis='y', stackdir='center', stackratio=1, dotsize=1, binwidth=0.4, show.legend=FALSE) + coord_cartesian(ylim=c(40, 60)) + labs(title="Variabilità osservata nella produzione tra le macchine", x="Macchina impiegata", y="Produzione realizzata") + theme_classic() + stat_summary(fun.data=mean_sdl, fun.args = list(mult=2), geom="pointrange", color="black", show.legend=FALSE) # aggiunge media +/- 2 deviazioni standard

#

Da notare che nella funzione stat_summary l'argomento mult=2 che specifica di rappresentare attorno alla media l'intervallo uguale a 2 deviazioni standard può essere modificato. 

La rappresentazione grafica dei dati ci viene nuovamente in aiuto nell'interpretazione dei risultati: come si vede i dati sono poco dispersi, le medie sono ben differenti, gli intervalli media ± 2 deviazioni standard non si sovrappongono, e questo conferma la significatività delle differenze tra le medie.

Dal punto di vista statistico è interessante notare l'importanza del disegno sperimentale. Quello qui adottato prevedeva di raccogliere i dati in modo tale che la variabilità osservata è quella dovuta al fattore macchina+operatore, pertanto non è possibile stabilire se le differenze (tra medie) osservate sono imputabili alla sola macchina, al solo operatore o a entrambi.

Impiegando un altro disegno sperimentale, e raccogliendo i dati diversamente, è possibile decomporre la variabilità osservata in variabilità dovuta al fattore macchina e variabilità dovuta al fattore operatore. lo facciamo nel post Analisi della varianza a due fattori, al termine del quale trovate anche alcune considerazioni generali sull'ANOVA.

----------

[1] Armitage P. Statistica medica. Giangiacomo Feltrinelli Editore, Milano, 1979, p. 188.

[2] Wonnacott TH, Wonnacott RJ. Introduzione alla statistica. Franco Angeli Editore, Milano, 1980, ISBN 88-204-0323-4, p. 237.

[3] Armitage P. Statistica medica. Giangiacomo Feltrinelli Editore, Milano, 1979, pp. 195-196.

[4] Vedere il post Come valutare l'omogeneità tra varianze.

[5] Snedecor GW, Cochran WG. Statistical Methods. The Iowa State University Press, 1980, ISBN 0-8138-1560-6. Chapter 15 - Failures in the assumptions, pp. 274-297.

[6] Wonnacott TH, Wonnacott RJ. Introduzione alla statistica. Franco Angeli Editore, Milano, 1980, ISBN 88-204-0323-4, Tabella 10-1, p. 238.

[7] Vedere il post Test parametrici e non parametrici per due campioni indipendenti.

[8] Vedere il post Test parametrici e non parametrici per più campioni indipendenti per il significato di queste correzioni, che controbilanciano l'aumento della probabilità, derivante dall'esecuzione di confronti multipli, di considerare la differenza tra le medie di due campioni come significativa quando invece non è significativa.

[9] Un test statistico più conservativo a parità di condizioni produce come risultato un valore di p più alto quindi ci aspettiamo che a lungo andare fornisca un numero inferiore di differenze significative, mentre un test statistico meno conservativo a parità di condizioni produce come risultato un valore di p più basso quindi ci aspettiamo che a lungo andare fornisca un numero maggiore di differenze significative.

[10] Si rimanda al post Grafici a punti (dotplot), inoltre nel post Grafici a violino (violin plot) trovate anche come sovrapporre ai punti un grafico a violino o un grafico a scatola con i baffi (boxplot).